Pressure stands as a fundamental concept in fluid mechanics and thermodynamics, shaping our understanding of fluid behavior and system dynamics. Among its various forms, static pressure holds particular significance. In this article, we delve into the essence of static pressure, elucidating its importance, mathematical expressions, and applications across different fields. By clarifying the distinctions between static, dynamic, and total pressure, we aim to provide a comprehensive overview of how pressure influences engineering, science, and everyday life. From its role in assessing fluid flow to its applications in medical devices and aerodynamics, static pressure emerges as a cornerstone in diverse disciplines, offering insights crucial for optimizing system performance and advancing technology.
What is Static Pressure?
Static pressure represents the pressure a fluid exerts perpendicular to any surface with which it is in contact. Static pressure can be measured using a piezometer.
Static pressure equation
Static pressure can be represented as a term in the Bernoulli equation. That equation, expressed in Eq. (1), illustrates the link between pressure, velocity, and elevation in fluid flow, representing energy conservation. According to the Bernoulli equation, the total mechanical energy per unit mass remains constant throughout the flow path for an ideal, incompressible fluid travelling along a streamline. In the Bernoulli equation, the term P (Pa) refers to static pressure, ρ (kg/m3) represents the density of the fluid, V (m/s) is the velocity of the fluid at that point, g (m/s2) is the acceleration due to gravity, and h (m) indicates the height above a reference point.
![\[ P+\frac{1}{2}pV^2+pgh = constand (1) \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-e00a3e19516739b86acd197f38b7b378_l3.svg "Rendered by QuickLaTeX.com")
Applications of static pressure
Static pressure is relevant in a wide range of applications across various fields. Some of the key applications include:
- Fluid mechanics: Static pressure is essential for assessing fluid flow in pipes, channels, and hydraulic systems in fluid mechanics. It makes it possible for engineers to build and operate fluid systems more effectively by assisting them in understanding pressure distributions, flow patterns, and energy losses.
- Medical Devices: Static pressure readings are used in medical devices like ventilators and respiratory equipment to oversee and control airflow to patients. Accurate regulation of static pressure is crucial for ensuring patient comfort and optimizing the effectiveness of therapy.
- Aerodynamics: Airplanes’ design and performance analysis depend on static pressure. It affects lift and drag forces on aircraft surfaces, which impacts flight efficiency, control, and stability.
Additionally, static pressure is a vital parameter in industrial processes, weather forecasting, HVAC systems, and various other applications.
What is dynamic pressure?
Dynamic pressure, or velocity pressure, measures a moving fluid’s kinetic energy per unit volume. Dynamic pressure P (Pa) is calculated using ρ (kg/m3), the density, and V (m/s), the velocity of the fluid, as in Eq (2).
![\[ P_d_y_n_a_m_i_c = \frac{1}{2}pV^2 (2) \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-6fa247aae0466e1d0dd6832e8d4c7b1d_l3.svg "Rendered by QuickLaTeX.com")
What is total pressure?
Total pressure, or stagnation pressure, is the sum of a fluid’s static and dynamic pressure flowing in a pipe or duct. It represents the fluid’s total energy per unit volume at a particular point in the flow field. Total pressure can be measured using a Pitot tube.
![\[ P_t_o_t_a_l = P_s_t_a_t_i_c\frac{1}{2}pV^2 (3) \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-4a302b26e6e232cabd0adc861ceac80e_l3.svg "Rendered by QuickLaTeX.com")
Static Pressure Vs. Dynamic Pressure Vs. Stagnation Pressure
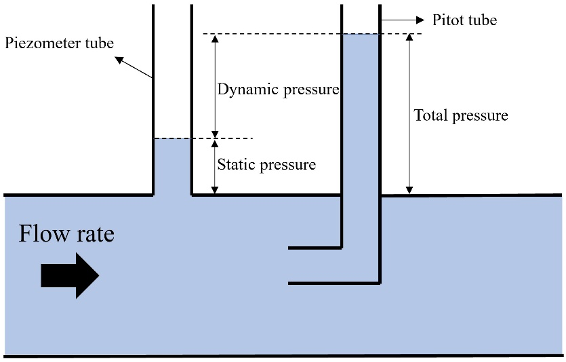
In Fig. 1, the fluid column height in the piezometer tube and pitot tube represent static and total pressures of the fluid flow, respectively. The difference between the mentioned columns’ heights is called dynamic pressure. By placing the height of each part h (m) in Eq. (4), the corresponding pressure P (Pa) is calculated. ρ (kg/m3) is the density of the fluid, and g (m/s2) is the acceleration due to gravity. Note that those pressures are gauge pressures and are related to atmospheric pressure.
![\[ P = p.g.h (4) \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-ad0fcb3508ad6e0cccfb2fe9e9acdac5_l3.svg "Rendered by QuickLaTeX.com")
Fig. 1. Measuring different types of pressure
An example of how to compute and use static pressure
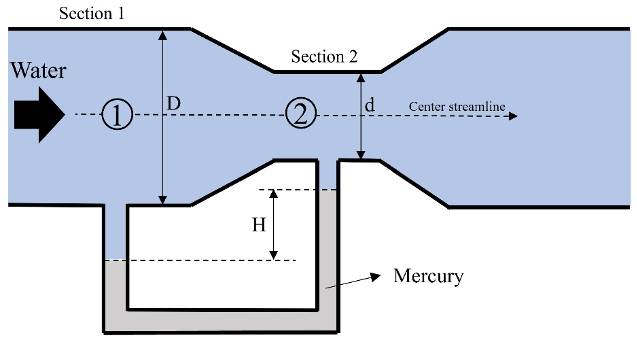
A venturi tube is illustrated in Fig. 2. The flow velocity at point 1 can be computed using the static pressure difference between points 1 and 2.
A Venturi tube is a device used in fluid mechanics to measure the flow rate of a fluid passing through a pipe. It consists of a narrow throat section connected between two larger diameter sections. As fluid flows through the Venturi tube, the narrowing of the throat causes the fluid velocity to increase, leading to a decrease in pressure according to Bernoulli’s principle. This pressure drop is measured and used to calculate the flow rate of the fluid. Venturi tubes find applications in various industries, including water treatment, HVAC systems, and aviation, where precise flow measurement is essential for efficiency and safety.
Fig. 2. A venturi tube
Bernoulli’s equation is assumed to hold along the center streamline:
![\[ P_1 +\frac{1}{2}p_W_a_t_e_rV_1^2 +p_W_a_t_e_rgh_1 = P_2 +\frac{1}{2}p_W_a_t_e_rV_2^2 +p_W_a_t_e_rgh_2} (5) \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-e6d5ed356bb0c1efcc1a21a0b86e788f_l3.svg "Rendered by QuickLaTeX.com")
If the tube is horizontal, h1 and h2 are equal, and we can solve for V1:
![\[ V_1^2-V_2^2 = 2p_W_a_t_e_r(P_2-P_1) (6) \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-a94bbd50d40617d4b93a896e1f029db8_l3.svg "Rendered by QuickLaTeX.com")
We relate the velocities from the incompressible continuity relation:
![\[ V_1A_1=V_2A_2=>V_1(\frac{\pi D^2}{4})=V_2(\frac{\pi d^2}{4})=>V_2=V_1\frac{D^2}{d^2} (7) \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-7a8749243d0a2ab5562b947d504e98d4_l3.svg "Rendered by QuickLaTeX.com")
According to the height of the mercury column, the pressure difference between point 1 and 2 is determined:
![\[ P_2-P_1 = p_m_e_r_c_u_r_ygH (8) \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-1aac205819b316e65d5beea2e3aefdb2_l3.svg "Rendered by QuickLaTeX.com")
Using equations (6), (7) and (8), the velocity at point 1 is:
![\[ V_1=(\frac{2p_w_a_t_e_r(p_m_e_r_c_u_r_ygH)}{1-\frac{D^4}{d^4}})^\frac{1}{2} \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-28fbcb1a4a668e840963aca67729baad_l3.svg "Rendered by QuickLaTeX.com")
What is relative pressure?
Relative pressure refers to pressure measurements taken relative to a specific reference pressure level. This reference pressure can be any defined pressure point or condition. For example, gauge pressure is a form of relative pressure, as it is measured relative to atmospheric pressure.
What is gauge pressure?
Gauge pressure is pressure measurements relative to a reference atmospheric pressure. it indicates the pressure above atmospheric pressure. Note that gauge pressure is positive for pressures over atmospheric pressure, while it is negative for pressures below atmospheric pressure.
What is absolute pressure?
The term absolute pressure describes the overall pressure that a fluid exerts, including the fluid’s internal pressure and the pressure of the surrounding air. It is the sum of the atmospheric pressure and the gauge pressure.
What is operating pressure?
In ANSYS FLUENT, operating pressure acts as a reference pressure. The default value is set to atmospheric pressure, which is 101325 Pa. The relation between operating pressure, absolute pressure and gauge pressure is defined as:
![\[ P_a_b_s_o_l_u_t_e = P_o_p_e_r_a_t_I_n_g +P_g_a_u_g_e (10) \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-177defb615a33fc2cf6405591bae9b6f_l3.svg "Rendered by QuickLaTeX.com")
Operating pressure determines the density in incompressible ideal gas flows and is important in avoiding roundoff error problems in low-Mach-number compressible flows. Therefore be sure to set the operating pressure appropriately.
Use Table 1 to set the operating temperature value in ANSYS FLUENT.
Table 1. Recommended Settings for Operating Pressure
| Density Relationship | Mach Number Regime | Operating Pressure |
| ideal gas law | M>0.1 | 0 or Almost mean flow pressure |
| ideal gas law | M<0.1 | Almost mean flow pressure |
| profile function of temperature | incompressible | not used |
| constant | incompressible | not used |
| Incompressible ideal gas law | incompressible | Almost mean flow pressure |
What is the pressure coefficient?
The pressure coefficient (Cp) is a dimensionless parameter utilized in fluid dynamics to characterize the pressure distribution surrounding an object submerged in a fluid flow. It is defined in equation 11.
In aerodynamics, Cp serves as a fundamental tool for analyzing airfoil performance. It provides insights into how pressure fluctuates across the airfoil’s surface, aiding in predicting lift and drag forces.
![\[ C_p = \frac{P-P_}{\frac{1}{2}pV^2} (11) \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-62d8894adaaf95a184eaef31ed6a0389_l3.svg "Rendered by QuickLaTeX.com")
Cp is the pressure coefficient, P is the static pressure at a specific point, P∞ is the free-stream static pressure, 𝜌 the fluid density, and V is the free-stream fluid velocity.
Conclusion
In conclusion, static pressure emerges as a foundational concept in fluid mechanics, serving as a cornerstone in understanding pressure distributions, flow dynamics, and energy conservation. Defined as the pressure exerted by a fluid at rest, static pressure finds widespread application across diverse fields, from aerospace engineering to medical device design. Crucially, static pressure is intricately linked to the Bernoulli equation, which illustrates the interplay between pressure, velocity, and elevation in fluid flow. Additionally, the distinction between static, dynamic, and total pressure provides insight into the various facets of fluid behavior. It enables engineers and scientists to optimize system performance in applications ranging from HVAC systems to aerodynamics. This article underscores its significance and relevance in engineering, science, and everyday life by comprehensively exploring the essence and applications of static pressure.