The discrete phase model (DPM) window in ANSYS Fluent is established from different sections.
As shown in Fig. 1, there is a separate tab entitled “ Physical Models” which provides various options that can be taken into account while tracking each particle in Lagrangian framework. All sub-models will be introduced in-depth in the following. However, It would be a great help to mention briefly the fundamentals of Discrete Phase Model (DPM) governing equation in ANSYS Fluent.
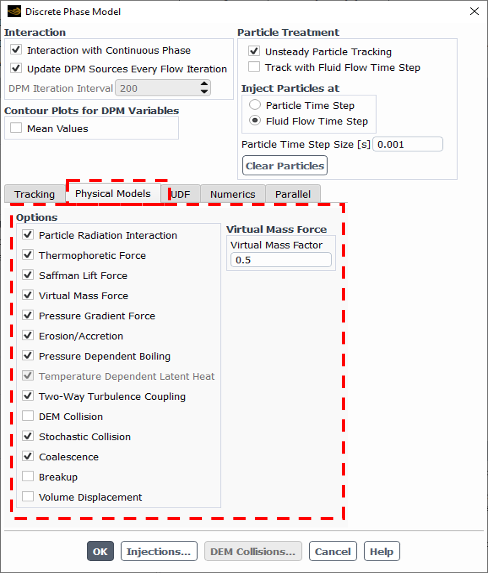
Figure 1: Discrete Phase Model (DPM) panel in ANSYS Fluent
In fact, the Discrete Phase Model in ANSYS Fluent predicts the trajectory of a discrete phase particle (such as a droplet or bubble) by integrating the force balance on the particle. This force balance is written in a Lagrangian reference frame and equates the particle inertia with the forces acting on the particle. For instance, the x-direction in Cartesian coordinates can be written as:
![\[ \frac{du_p}{dt} = F_D(u - u_p) + \frac{g_x(\rho_p - \rho)}{\rho_p} + F_x \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-12fed8b88014566ff097893c8f036e72_l3.png "Rendered by QuickLaTeX.com")
Where:
- The first term on the right side represents the drag force per unit particle mass.
- The second term accounts for the gravity effect and buoyancy force.
- Fx represents additional forces that may be important under special circumstances
*** The discrete Phase Model physical models mainly focus on additional forces that are applied by the Fx term in the governing equation. Given this short introduction, we can investigate each option provided in the discrete phase model physical model Tab.
Physical Models for the Discrete Phase Model
Particle Radiation Interaction
The “ Particle Radiation Interaction “ model is particularly valuable in applications where radiation plays a prominent role in thermal processes, such as in combustion chambers. ANSYS Fluent calculates the radiative heat transfer to and from the dispersed phase (particles) when this model is activated. Needless to say, this interaction can influence the temperature of both the particles and the fluid, affecting the overall dynamics of the flow.
*** This option will be available only if P1 or Discrete Ordinates (DO) radiation model is activated.
Furthermore, two extra radiative properties, including Particle emissivity and scattering factor, must be specified for particle materials, as depicted in Fig. 2. Particle emissivity defines the ability of a particle to emit radiation. It is a dimensionless number ranging from 0 to 1. A value of 1 means the particle is a perfect emitter (blackbody), while 0 means it does not emit any radiation. According to ANSYS Help, particle emissivity is 1 for coal particles and 0.5 for ash.
Moreover, 0.95 is estimated for water droplets. Similarly, the particle scattering factor defines how much radiation is scattered by the particle. It is also a dimensionless number between 0 and 1. A value of 0 means the particle does not scatter radiation at all, while a value of 1 means the particle scatters all incident radiation. The particle scattering factor highly depends on the size of the particle. As a rule of thumb, it is 0 for soot particles and 0.5-1 for water droplets.
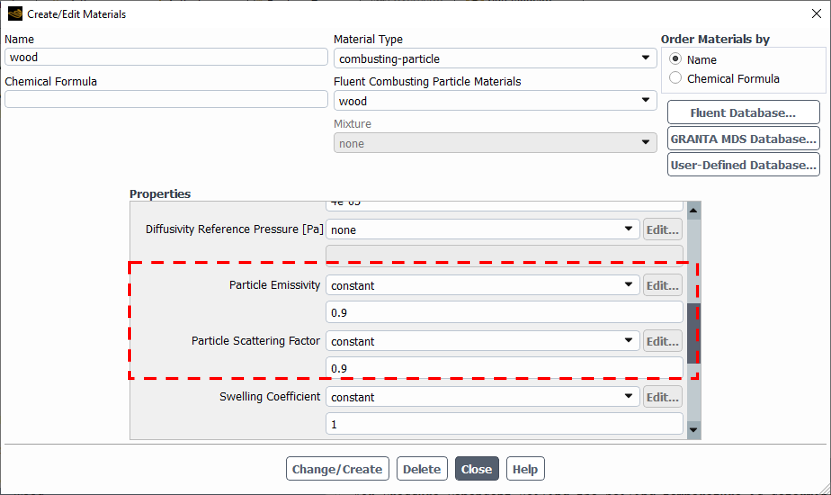
Figure 2: Particle emissivity and Particle scattering factor in the particle material properties section of ANSYS Fluent
Thermophoretic Force
The thermophoretic force in the Discrete Phase Model (DPM) physical model refers to the force exerted on particles due to a temperature gradient in the surrounding fluid. Physically, the force is applied due to the difference in momentum transfer between gas molecules and the particles on the hotter and cooler sides.
Molecules from the hotter side have more kinetic energy and impart more momentum to the particle, pushing it toward the cooler side. Thus, thermophoretic force should be included as an additional force in problems with a dominant high-gradient temperature.
Mathematically, the additional force of Fth is defined as:
Where:
Ft is the thermophoretic force acting on the particle.
Ct is a constant (typically around 1.17).
μ is the dynamic viscosity of the fluid.
dp is the particle diameter.
∇T is the temperature gradient.
T is the absolute temperature of the fluid.
*** As can be seen in Fig. 3, ANSYS Fluent uses talbot-diffusion model to predict thermophoretic coefficient. This model is a function of particle size and gas properties, providing a more accurate description of the thermophoretic force.
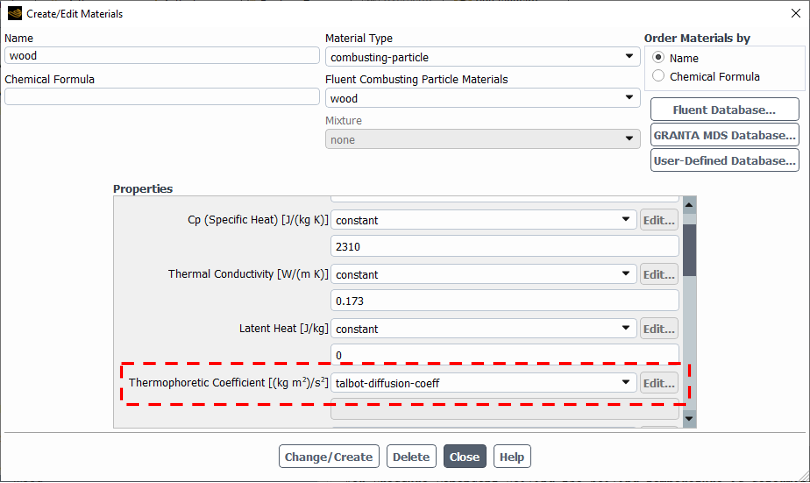
Figure 3: Thermophoretic coefficient model in ANSYS Fluent
Saffman Lift Force
The Saffman Lift Force in the Discrete Phase Model (DPM) physical model refers to a force that acts on particles moving through a fluid when there is a velocity gradient (shear) in the surrounding flow. Under this condition, the particle experiences a lift force perpendicular to the flow’s direction. We don`t get into the mathematical formulation here. The most notable point about the inclusion of saffman lift force is that it t is most significant for small particles (in the micron range and below) and becomes negligible for larger particles where other forces, such as drag, dominate.
Virtual Mass Force and Pressure Gradient Force
These two forces are also given in terms of options in Discrete Phase Model Physical Models. Virtual Mass Force and Pressure Gradient Force must be activated to improve the prediction of particle dispersion in cases where:
Density of continuous phase >= Density of Discrete phase
A common example is bubbles dispersed in liquid flow. Scientifically, the virtual mass force arises when a particle accelerates within a fluid. It accounts for the additional inertia the fluid exerts on the particle due to its motion. Additionally, The virtual mass factor in Fluent determines the influence of the virtual mass force on particles, with a value of 1 applying the standard force, values greater than 1 increasing the force’s effect, and values less than 1 reducing it (see Fig. 4).
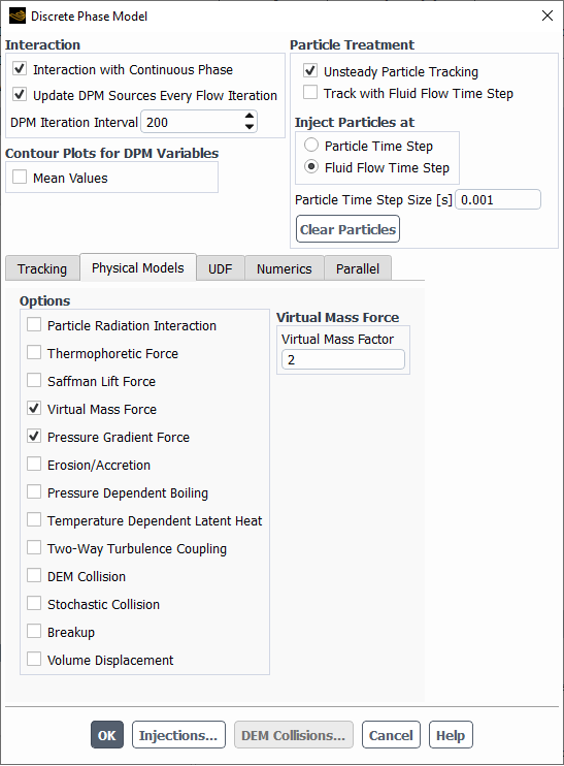
Figure 4: Virtual mass factor in DPM panel
Likewise, in cases where the density ratio is above 1, the pressure gradient effects have to be considered by activation of Pressure Gradient Force option.
Erosion/Accretion
The erosion/accretion option in DPM physical model provides a framework for simulating complex interactions between particles and walls. So the erosion and accretion rates will be calculated on wall boundaries. Among many theoretical formulations, ANSYS Fluent offers five erosion models including Finnie, Generic, Oka, Mclaury and DNV. This sub-model requires an independent article for further details. For now, you can check out the practical investigation of erosion provided in the CFD Shop.
Figure 5: Erosion In Air-cooled Condenser (ACC) CFD Simulation, ANSYS Fluent Training
Pressure Dependent Boiling
The boiling point of a liquid is the temperature at which its vapor pressure equals the surrounding pressure. Pressure-dependent boiling refers to the phenomenon where the boiling point of a liquid varies with changes in pressure. As pressure increases, the boiling point also increases. Conversely, as pressure decreases, the boiling point decreases. So, in simulations where pressure deviates from atmospheric levels, it’s essential to adjust the boiling point to align with the average pressure. Enabling Pressure dependent boiling option, ANSYS Fluent allows a switch from droplet vaporization (Law 2) to boiling (Law 3) based on the local conditions.
By default, ANSYS Fluent transitions from vaporization to boiling when the particle temperature reaches the predefined boiling point for the droplet material. However, with the Pressure Dependent Boiling option enabled, this transition condition changes to reflect the saturation vapor pressure at the droplet temperature compared to the domain pressure (Psat>P). Suppose the domain pressure exceeds the saturation vapor pressure while in the boiling law, the model will revert to the vaporization law.
It is crucial to provide accurate droplet saturation vapor pressure data (Fig. 6) that covers the entire pressure and temperature range of your simulation. Last but not least, When Pressure Dependent Boiling is enabled, then the Temperature Dependent Latent Heat model automatically applies.
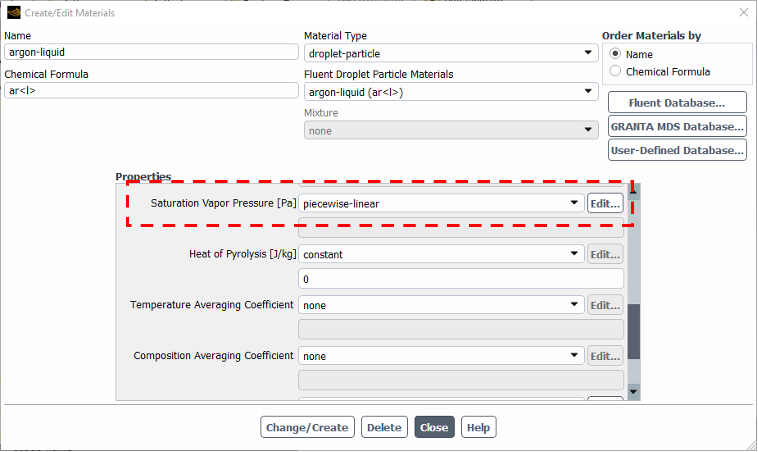
Figure 6: saturation vapor pressure when using Pressure dependent boiling model
Two-way Turbulence Coupling
In cases where the dispersed phase also affects the continuous phase turbulence, the Two-way turbulence coupling option can lead to a more realistic approach. As ANSYS guide stated, this option enables the effect of change in turbulent quantities due to particle damping and turbulence eddies.
DEM Collision
DEM Collision refers to the Discrete Element Method (DEM) collision modeling. This approach simulates the behavior of granular materials and particles. So, wherever the flow is characterized by a high volume fraction of dispersed phase, DEM collision is crucial. In other words, the high volume fraction of particles leads to continuous particle-particle interactions. In theoretical concepts, this approach is known as 4-way DPM coupling:
- Continuous phase effect on Discrete Phase
- Discrete Phase effect on Continuous phase
- Discrete Phase effects on itself (particle-particle interaction)
ANSYS Fluent DEM Collision model enables further windows to describe collision partners, contact force laws, etc (see Fig. 7). All of the parameters will be discussed in another independent article.
*** ANSYS introduced a new extension named ANSYS Rocky that is designed for particulate flow and specializes in simulating the behavior of granular materials and particles. It is particularly strong in applications involving discrete element modeling (DEM).
Figure 7: DEM Collision in Discrete Phase Model Physical Models of ANSYS Fluent
Stochastic Collision and Coalescence
Due to extremely high computation cost of DEM collision model, ANSYS fluent offers an alternative. Stochastic collision and coalescence are simpler, more efficient methods for handling particle interactions, use statistical models and averages, and do not simulate detailed mechanics. The coalescence sub-model will be shown if only stochastic collision is activated. In fact, coalescence refers to the process where two or more particles merge to form a single larger particle upon collision. This is particularly relevant in systems where the growth of droplets or bubbles is important, such as in spray or emulsion flows.
Technically, after collision of two particles , ANSYS algorithm determines the type of collision. For liquid droplets, coalescence and bouncing outcomes are considered, while for solid particles, only bouncing is considered. The probability of an outcome is calculated from the collisional Weber number. The Weber number (We) is a dimensionless number that characterize the relative importance of inertial forces to surface tension forces.
![\[ We = \frac{\rho u^2 L}{\sigma} \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-ccf76638a0a6662a54439cbf64319361_l3.png "Rendered by QuickLaTeX.com")
ρ = Density of the fluid (kg/m³)
u = Characteristic velocity of the fluid (m/s)
L = Characteristic length (typically the diameter of the droplet or particle) (m)
σ = Surface tension of the fluid (N/m)
*** Tips:
- If the particle time step is excessively large, the results may become influenced by that time step. Therefore, it’s advisable to appropriately adjust the particle length scale.
- This model is best suited for low-Weber-number collisions, where interactions typically lead to bouncing or coalescence (We<100).
Breakup
Breakup refers to the process of droplet distortion as it moves. ANSYS Fluent professionally adopted breakup models for users to consider breakup for any injection. Briefly, by enabling the breakup option in the physical model panel, six different breakup models will be shown in the injection window including TAB, Wave, KHRT, SSD, Madabhushi and Schmehl, as depicted in Fig.8. All the models plus the breakup theory of the droplets will be discussed in an independent article regarding the vast theory and assumptions.
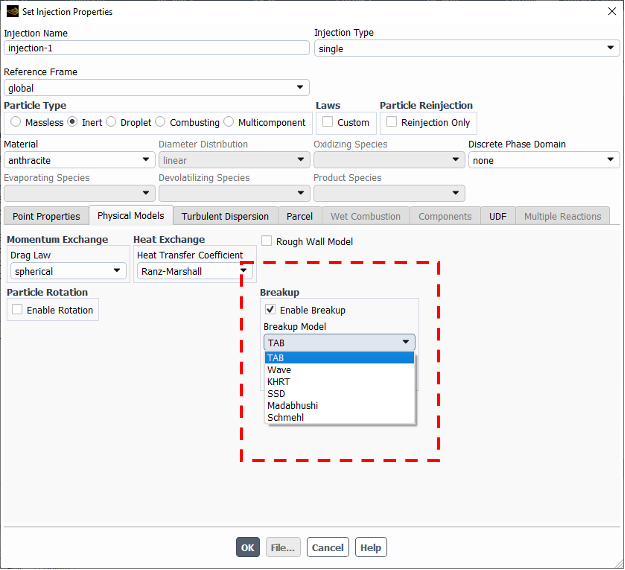
Figure 8: Breakup models in DPM
Volume Displacement
Volume Displacement refers to the effect that discrete particles have on the continuous phase by occupying space within the fluid domain. When particles take up a significant volume, they displace the fluid, which is what ANSYS presents as a blockage effect. Therefore, enabling volume displacement option means considering blockage effect. This effect is often negligible in dilute particle flows (very low-volume fractions).
The user can set the maximum particle volume fraction used to compute the continuous phase volume fraction by the following command:
- define/models/dpm/interaction> max-vf-allowed-for-blocking
- Maximum DPM volume fraction used in continuous flow (0 1.) [0.95]
- According to the ANSYS user guide, 0.95 is recommended.
You can get access to dpm cfd
read more: