The Finite Element Method (FEM) stands as a cornerstone in the realm of engineering and scientific simulations, offering a powerful framework for tackling complex physical phenomena. Rooted in the discretization of space- and time-dependent problems expressed by partial differential equations (PDEs), FEM provides a versatile numerical approach to approximate these equations through the division of problem domains into finite elements.
Contents
ToggleThis article delves into the foundational principles, historical evolution, diverse applications, and future prospects of FEM, shedding light on its significance in engineering design, scientific research, and computational analysis. From its inception to contemporary advancements, FEM continues to revolutionize how we understand and simulate the intricate interplay of forces, materials, and processes shaping our world.
What is the Finite Element Method?
The description of the laws of physics for space- and time-dependent problems are usually expressed in terms of partial differential equations (PDEs). In many cases, traditional analytical methods struggle to solve PDEs due to the complexity of the geometries and problems. Instead, we turn to numerical methods that approximate these equations through discretization.
The Finite Element Method (FEM) is one such approach. It breaks down the problem domain into finite elements, which are small, manageable pieces. These elements are governed by simpler equations, allowing us to solve the overall problem numerically.
However, it’s important to note that the solutions obtained through FEM are approximations of the true solutions to the PDEs. FEM provides a practical way to tackle complex problems, but the results are inherently approximate due to the discretization process.
Applications of the Finite Element Method
FEM has practical applications in every scientific or engineering discipline that involves PDEs. FEM finds applications across various fields due to its adaptability and capacity to tackle challenging issues. Well-known applications of FEM include structural analysis, heat transfer, fluid dynamics, electromagnetism, manufacturing and material design, biomechanics and biomedical engineering, acoustics and vibrations, and multiphysics simulation. These applications underscore FEM’s extensive applicability across various fields and disciplines, solidifying its status as a vital tool for engineers, scientists, and researchers.
History of the Finite Element Method
The concept of representing a domain as discrete parts has historical roots dating back to ancient mathematicians. In modern times, this idea has found practical application in aircraft structural analysis, where components like wings and fuselages are treated as assemblies of discrete elements. In 1941, Hrenikoff introduced the framework method, representing a plane elastic medium as a collection of bars and beams.
Courant’s work in 1943 further utilized piecewise-continuous functions over subdomains to approximate unknown functions, as seen in the study of the St Venant torsion problem using triangular elements. The formal presentation of the Finite Element Method is attributed to Argyris and Kelsey in 1960 and to Turner, Clough, Martin, and Topp in 1956. The term “finite element” was first coined by Clough in 1960. Since then, the literature on finite element applications has grown exponentially, with numerous journals dedicated to its theory and application. The number of papers has gone from one (1956) to more than a million (2022).
The 1980s and 1990s witnessed the widespread commercialization of FEM software, making it accessible to engineers and researchers across various fields. FEM found applications in civil engineering, geotechnical engineering, nuclear engineering, and more. In recent decades, FEM has seen continuous advancements, including parallel computing, adaptive mesh refinement, and multiphysics simulation capabilities.
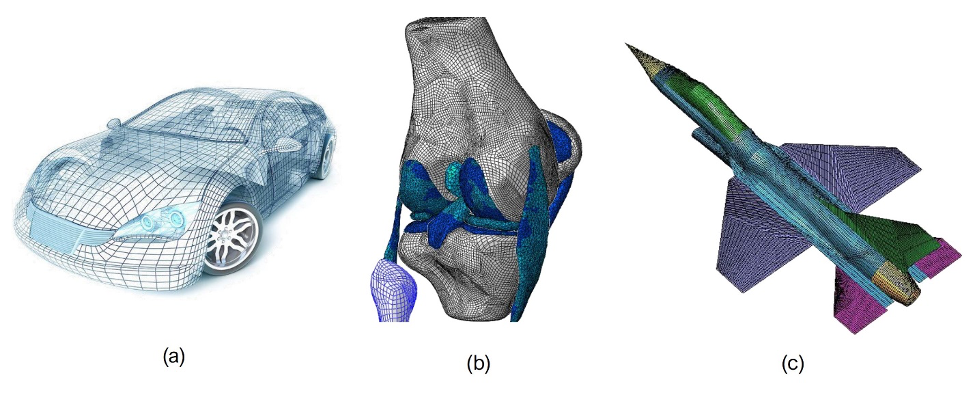
the discretization of: (a) a car, (b) a human joint, and (c) a F-16 aircraft. From solution to engineering problems using finite element method by Vijak Goyal et al.
How Does FEM Work?
The Finite Element Method (FEM) operates by breaking down the problem domain into smaller, more manageable elements like triangles or tetrahedra in 2D or 3D space, respectively. Each of these elements is linked to a set of nodes, and the behavior of the system within each element is approximated using mathematical interpolation functions.
This subdivision of the domain into finite elements allows FEM to convert the original continuous problem into a system of algebraic equations that can be solved using numerical techniques. After discretizing the problem domain, the subsequent step in FEM involves formulating the governing equations for each element. These equations are based on fundamental physical principles, such as equilibrium equations for structural analysis or conservation laws for fluid dynamics. Typically, the behavior within each element is approximated using polynomial basis functions, and boundary conditions are applied to ensure solution compatibility.
Once the equations for each element are established, they are combined into a global system of equations representing the behavior of the entire problem domain, taking into account the connectivity between elements through shared nodes. Subsequently, the global system of equations is numerically solved to determine the solution variables, such as displacements, stresses, strains, temperatures, or other relevant parameters. Various numerical methods, including direct solvers, iterative solvers, or matrix factorization techniques, can be utilized for efficient solution computation. Finally, the obtained solution is analyzed and visualized through post-processing, providing valuable insights into the system’s behavior and aiding in engineering design and decision-making processes.
What are the Different Types of Finite Element Method?
The core Finite Element Method (FEM) is a strong approach. However, it varies based on its challenges and applications. Here are some common forms of FEM:
- Extended Finite Element Method (XFEM): This method is useful when analysing systems with discontinuities and jumps that cannot be directly handled by the finite element method, such as fractures. XFEM enriches the element shape functions to account for these discontinuities, providing more accurate solutions. This can be advantageous in certain cases, especially when the discontinuities move or evolve during the simulation.
- Generalized Finite Element Method (GFEM): It integrates aspects of both traditional Finite Element Method and meshless methods. An advantage of GFEM is its ability to avoid the need for re-meshing around singularities, making it particularly useful for problems involving discontinuities or localized features.
- Mixed FEM: It is particularly suited for problems featuring contact or incompressibility, where constraints are enforced using Lagrange multipliers. In MFEM, both primary variables and auxiliary variables, which represent the Lagrange multipliers, are approximated simultaneously using different finite element spaces. These additional degrees of freedom from Lagrange multipliers are treated independently within the solution process. The system of equations in MFEM is solved as a coupled system, where the primary and auxiliary variables interact to ensure compatibility and accuracy in representing the underlying physics of the problem. MFEM’s ability to handle coupled systems efficiently makes it a powerful tool for a wide range of engineering and scientific applications, particularly in scenarios involving complex constraints or interactions.
- hp-FEM: It combines automatic mesh refinement (h-refinement) with an increase in polynomial order (p-refinement). Unlike separate h- and p-refinements, hp-FEM allows elements to have different polynomial orders after subdivision. This method optimizes accuracy and computational efficiency for problems with localized features or sharp gradients.
- Discontinuous Galerkin FEM: It addresses limitations of traditional FEM in handling sharp discontinuities like shock waves and material interfaces. By employing non-overlapping elements with independent polynomial approximations within each element, DG-FEM directly incorporates these discontinuities. This approach makes it a powerful tool for solving hyperbolic equations governing wave propagation phenomena and excels in problems with bending or incompressible materials common in material processes.
Advantages and Disadvantages of FEM
The real world is full of interconnected physical phenomena. For instance, heat transfer can affect material properties and vice versa. FEM allows you to solve equations governing these diverse phenomena simultaneously within a single model. Traditional methods might require solving each physical phenomenon separately and combining the results. FEM creates a unified system where these equations are coupled, allowing for a more comprehensive analysis of how these phenomena interact.
Another significant aspect contributing to the success of the method is its capability to increase the order of elements effectively. This enhancement enables a more accurate approximation of the physics fields by locally representing them with higher-order polynomials, such as second and third-degree polynomials or higher. This refinement process is particularly critical in scenarios demanding precise stress analysis, where a finer resolution of the model is necessary to capture complex behaviours and variations accurately.
However, the finite-element method relies on advanced mathematical principles, necessitating expertise for its implementation. Proficiency in concepts like variational formulations, numerical integration, interpolation functions, and matrix algebra is essential. Additionally, computational skills and numerical analysis proficiency are crucial for devising efficient algorithms and selecting suitable solution strategies. A solid mathematical background is, therefore, essential for effective utilization of the finite-element method in engineering and scientific applications.
Future and challenges of FEM
The Finite Element Method is poised for significant advancements and expanded applications across engineering and scientific domains. Ongoing developments in high-performance computing, adaptive mesh refinement, multiphysics modelling, and uncertainty quantification promise to enhance FEM’s accuracy, efficiency, and versatility in simulating complex phenomena. Integrating emerging technologies like artificial intelligence, machine learning, and additive manufacturing offers the potential for revolutionizing design optimization, material development, and manufacturing processes. As interdisciplinary collaborations deepen and computational capabilities evolve, FEM will continue to lead engineering analysis and design, catalyzing innovation and facilitating breakthroughs in the foreseeable future.
One challenge simulation models face is the study of multi-scale phenomena, where small-scale events influence larger-scale processes. For instance, water vapour emissions from the sea surface can impact weather patterns. The hope is that advancements in simulation techniques will address these challenges in the coming years, enabling more accurate and comprehensive modelling of such complex interactions.
Some fields of FEM’s application to composites: (a)wind power, (b)sports, (c)automotive, (d)construction, (e)naval, (f)aeronautics, (g)space. From application of the finite elemen method in the analysis of composite materials by Sarah David Müzel et al.
Ansys Mechanical
Ansys Mechanical empowers users to solve intricate structural engineering challenges and optimize design decisions efficiently. Its suite of finite element analysis (FEA) solvers allows for customization and automation of solutions tailored to structural mechanics problems. Users can parameterize analyses to explore multiple design scenarios rapidly. Ansys Mechanical offers comprehensive analysis tools, ensuring versatility and accuracy in engineering simulations.
What is finite volume method?
The Finite Volume Method (FVM) is a numerical approach widely acclaimed for its inherent conservation property. It involves assessing volumes within discretized geometries.
It operates through a two-step process to translate Partial Differential Equations (PDEs) into linear algebraic equations. Initially, PDEs are reformulated and integrated across discrete elements, converting surface and volume integrals into discrete algebraic relationships using integration quadrature methods to achieve specified accuracy, resulting in a set of semi-discrete equations. Subsequently, the method estimates variations in variables within elements by selecting appropriate interpolation profiles, which are then connected to surface variables, ultimately transforming the algebraic relationships into fully discrete equations. This sequential approach not only ensures accuracy but also facilitates efficient computation in solving complex physical problems.
ANSYS Fluent, a leading computational fluid dynamics (CFD) software, relies on the Finite Volume Method to numerically solve diverse fluid flow and heat transfer problems. By discretizing the computational domain into control volumes and transforming the governing equations into integral forms, ANSYS Fluent effectively captures the behavior of fluid flow variables such as velocity, pressure, and temperature. Through iterative solution algorithms and boundary condition enforcement, Fluent accurately predicts flow phenomena at various scales, from turbulence modeling to multiphase flows.
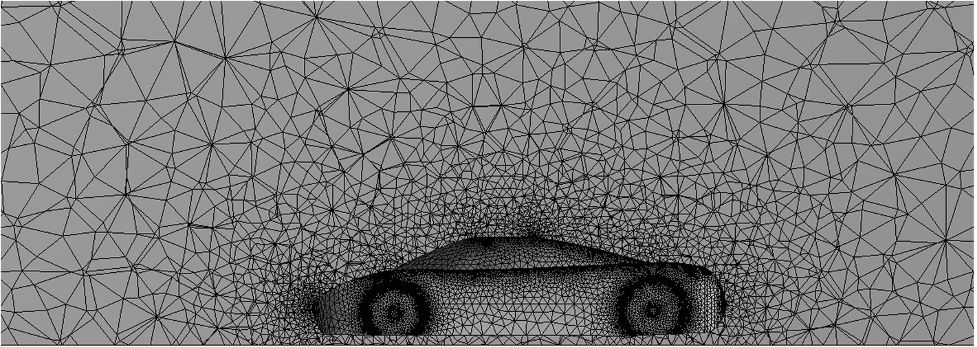
Meshed model for Aerodynamics analysis of a vehicle. From “Drag reduction by application of aerodynamic devices in a race car” by Devang S. Nath et la. Developed using ANSYS Mesh Tool
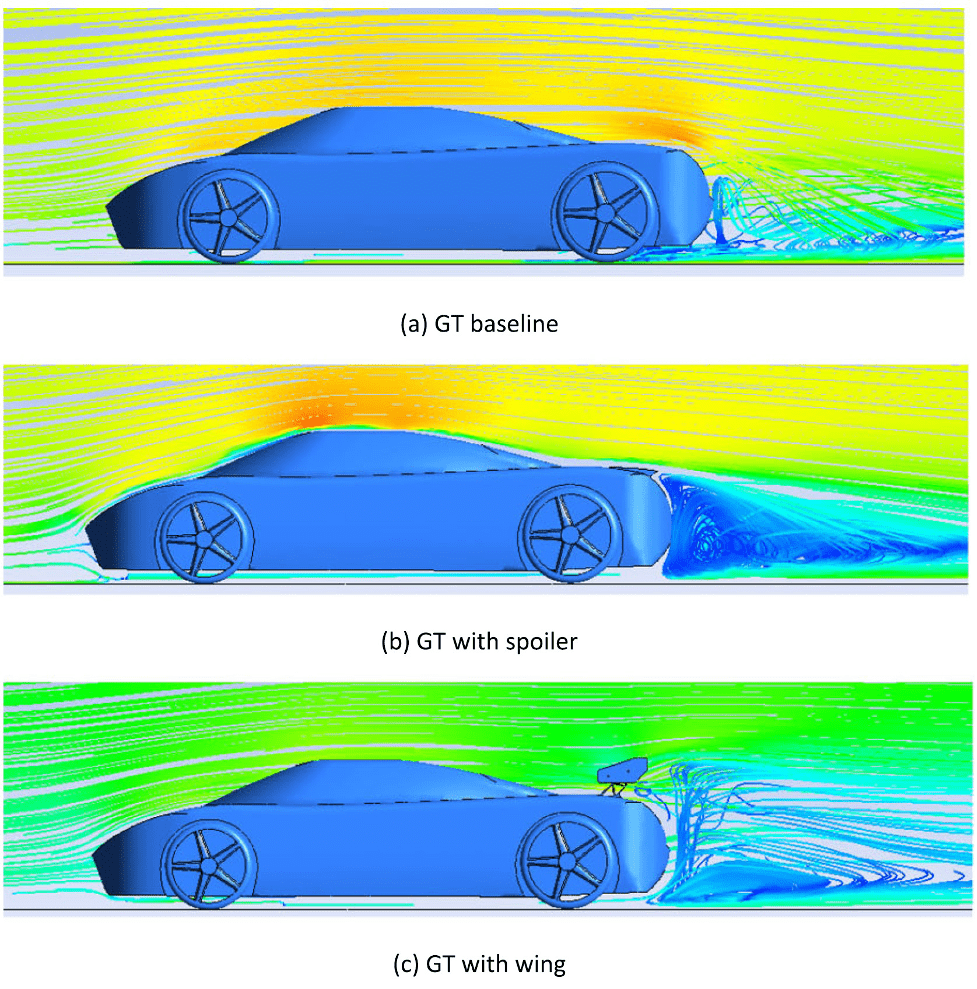
Streamlines after vehicle for different cases. From “Drag reduction by application of aerodynamic devices in a race car” by Devang S. Nath et la. Simulated in ANSYS Fluent
Advantages and Disadvantages of FVM
The Finite Volume Method boasts several advantages, making it a popular choice for solving a wide range of computational fluid dynamics problems. Firstly, its inherent conservation properties ensure accurate representation of mass, momentum, and energy conservation, crucial for realistic simulations of fluid flow, heat transfer, and other physical phenomena. FVM’s flexibility in grid generation allows for efficient handling of complex geometries through structured, unstructured, or hybrid grids, enhancing its applicability across diverse engineering domains. Additionally, FVM’s robustness and straightforward implementation make it accessible to engineers and researchers, enabling efficient solution of challenging problems while maintaining numerical stability and ease of use.
On the other hand, the Finite Volume Method also presents certain disadvantages that need to be considered. Achieving higher-order accuracy with FVM can be challenging compared to other numerical methods like Finite Element Method, limiting its ability to capture fine-scale features accurately. Moreover, while FVM’s conservation properties are advantageous, they can also restrict its flexibility in handling certain boundary conditions and dynamic scenarios, necessitating careful consideration of model setup and grid parameters to ensure accurate and reliable results.
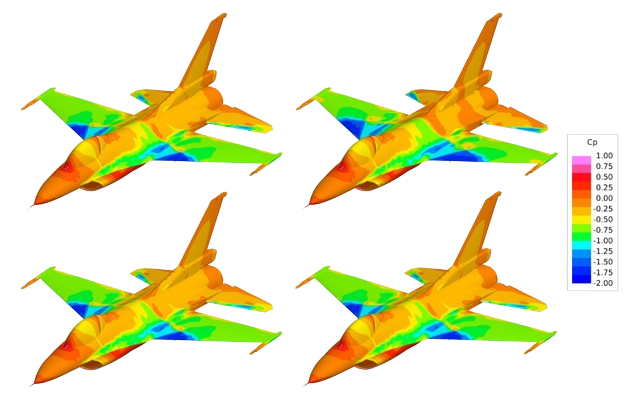
Pressure coefficient distributions over the A/C surface using various turbulence models, top view. From top left in clockwise order: Reference, SST, k-ω, k-ε Enhanced Wall Treatment, k- ε Menter-Lechner. From “Validation of Reynolds-Averaged Navier-Stokes Computations over a Fighter Aircraft with Experimental data” by Berk Sarıkaya et al. Simulated in ANSYS Fluent
The Finite Element Method (FEM) vs. The Finite Volume Method (FVM)
While both Finite Element Method (FEM) and Finite Volume Method (FVM) share similarities as systematic numerical approaches for solving Partial Differential Equations (PDEs), their ease of implementation sets them apart. Among engineers, Finite Difference Method (FDM) is often considered the easiest to implement, with FEM being the most challenging and FVM falling somewhere in between. The decision between FEM and FVM typically hinges on ease of use and implementation.
While some engineers argue for the superiority of FVM over FEM in Computational Fluid Dynamics (CFD) analysis due to its conservation properties and straightforward flux evaluation at boundaries, this debate lacks conclusive evidence, leaving the choice up to users. Ultimately, engineers weigh the advantages and disadvantages of each method to determine the most suitable approach for a given scenario. FVM is commonly favored for CFD problems involving conservation laws, as its flux evaluation at boundaries aligns well with the requirements of conservation principles
Conclusion
In conclusion, the Finite Element Method (FEM) stands as a versatile and indispensable tool in the realm of engineering and scientific simulations. From its inception rooted in the discretization of partial differential equations (PDEs) to its contemporary applications spanning across diverse fields, FEM has continually evolved to address complex challenges and propel innovation.
The historical evolution, diverse applications, and future prospects outlined in this article underscore the enduring significance of FEM in engineering design, scientific research, and computational analysis. With its ability to provide accurate and comprehensive solutions to interconnected real-world problems, FEM remains a cornerstone in driving engineering innovation and scientific discovery in the foreseeable future.