Boundary conditions play a pivotal role in various scientific and engineering disciplines, from fluid mechanics to electromagnetics and finite element analysis. They define the behavior of solutions to differential equations at the boundaries of a domain, reflecting real-world constraints and scenarios. This article provides an overview of boundary conditions in different fields, elucidating their significance and common types, along with practical examples from computational simulations using tools like ANSYS Fluent.
Contents
Toggle
Boundary conditions in differential equations
Differential equations that solely rely on initial conditions to determine their solutions are termed initial value problems. However, differential equations that necessitate additional constraints at the boundaries of the domain for their solution are known as boundary value problems. While initial conditions specify the state of the system at a single point or within a certain range at the initial time, boundary conditions dictate the behavior of the solution at the boundaries of the spatial domain. This distinction is crucial in mathematical modeling and is foundational in various fields, including physics, engineering, and applied mathematics.
Click to access the Combustion CFD
Boundary conditions meaning in physical systems
In physics, boundary conditions are essentially specifications for what happens at the edges of a system, like fixed ends on a vibrating guitar string. These act as constraints on mathematical models, often differential equations, and are crucial for narrowing down solutions to reflect real-world scenarios. They play a vital role in various areas like heat transfer, wave behavior, and structural analysis.
Boundary condition definition with an example
Equation 1 is a second-order differential equation.

Constraints (boundary conditions) on the solution y = y(x) at two values of x are:

The general solution to Equation 1 is:

Placing boundary conditions into the general solution:
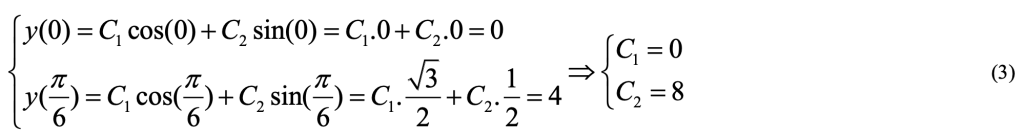
The one and only solution to our boundary value problem is:

Types of boundary conditions
There are numerous boundary conditions. The main types of boundary conditions are:
Dirichlet boundary condition
A Dirichlet boundary condition, also known as the first-type boundary condition, specifies the exact value that a quantity must take on the boundary of a domain in a differential equation. For example, consider a heat transfer problem involving a metal rod. A Dirichlet boundary condition would set a fixed temperature at one or both ends of the rod. This boundary condition constrains the possible solutions to the differential equation and reflects real-world scenarios where boundaries might have known, fixed values. For example, the boundary conditions stated for Equation 1 were of this type. As another example, Laplace’s equation and its related dirichlet boundary conditions with a rectangular domain with boundaries x=0, x=a, y=0 and y=b are:

Neumann boundary condition
Neumann boundary conditions, also known as the second-type boundary condition, specify the rate of change (often the flow) of a quantity at the system’s edge. Imagine heat flow instead of temperature. A Neumann condition on a metal rod would specify the constant heat flux, not the exact temperature, at the end. As an example, neumann boundary conditions for equation 5 with a rectangular domain with boundaries x=0, x=a, y=0 and y=b are:
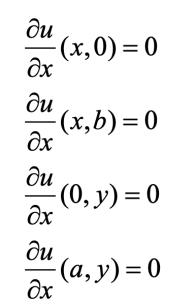
Robin boundary condition
Robin boundary conditions, also known as the third-type boundary condition, blend Dirichlet and Neumann conditions. They describe a situation where both the value of a quantity (like temperature) and its rate of change (flow) matter at the boundary. Imagine a cup of coffee cooling in air; a Robin condition considers both the temperature difference between the coffee and the air and the rate of heat transfer between them. In other words, it specifies a linear combination of the function and its derivative at the boundary. For equation 5, robin boundary condition is:

Cauchy boundary condition
A Cauchy boundary condition is indeed the most comprehensive, as it specifies both the precise value of a quantity and its rate of change at the boundary of a domain. For instance, envision a vibrating string anchored at one end. A Cauchy condition would not only define the fixed position of that end but also provide information about its initial velocity (i.e., how fast it’s moving) at that specific point. This level of detail is especially pertinent for hyperbolic problems, such as wave equations, where both the value and its change are imperative for comprehending wave propagation. it is a combination of dirichlet and neumann conditions. as an example, cauchy boundary condition for equation 5 is:

Mixed boundary condition
A mixed boundary condition arises when a system described by a differential equation has different boundary conditions applied to various parts of its border. For instance, envision a vibrating drumhead fixed at the rim but free to move in the center. In this scenario, separate sections of the boundary have different types of conditions, such as fixed position versus free movement. While this adds complexity, it enables more realistic modeling of scenarios where various constraints or interactions exist at different parts of the system’s edge. As an example, mixed boundary conditions for equation 5 with a rectangular domain with boundaries x=0, x=a, y=0 and y=b are:

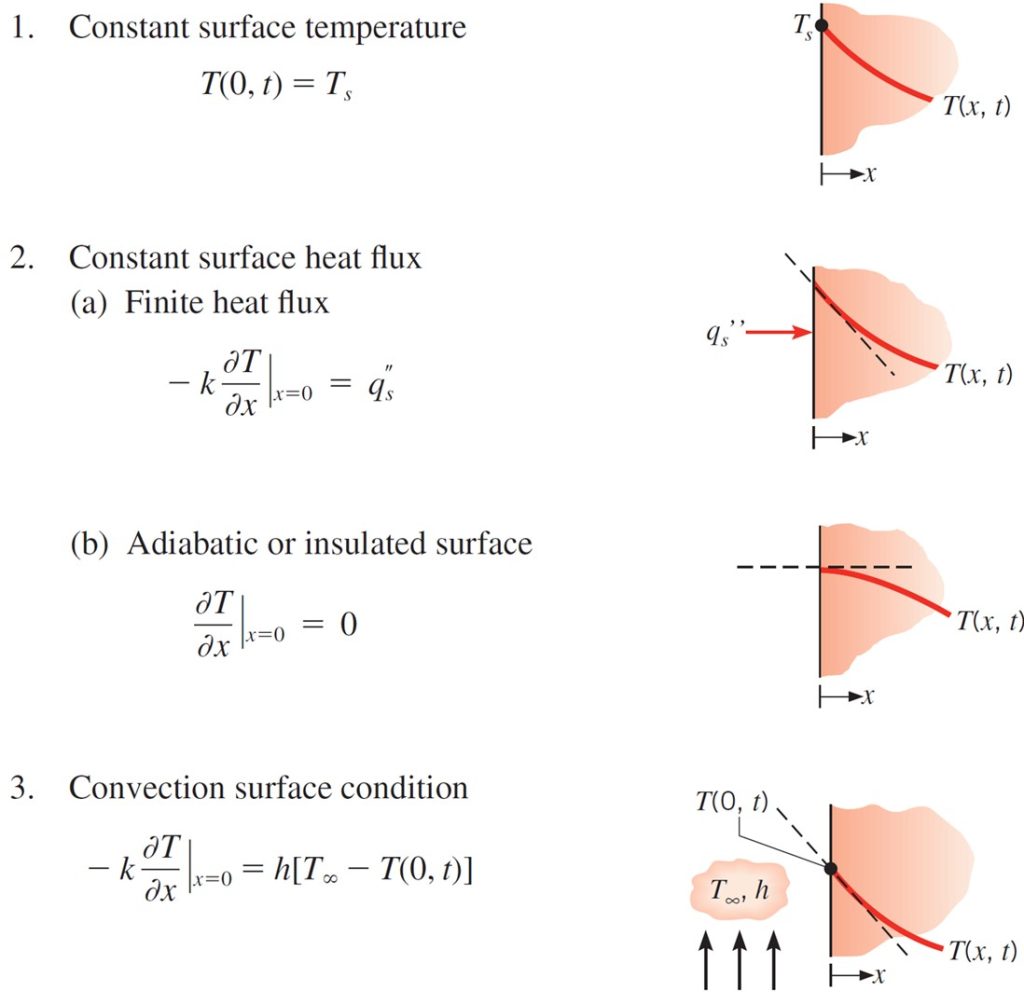
Boundary conditions for the heat diffusion equation at the surface. From fundamentals of heat and mass transfer by FRANK P. INCROPERA et al.
What are the boundary conditions in fluid mechanics?
In fluid mechanics, boundary conditions are the set of constraints or specifications applied at the boundaries of the fluid domain. These conditions define the behavior of the fluid at the boundaries and are essential for solving fluid flow problems. Here are some common types of boundary conditions in fluid mechanics:
No-slip boundary condition
The no-slip boundary condition in fluid dynamics dictates that at a solid boundary, the fluid velocity relative to the surface is zero. This implies that the fluid particles adhere to the surface, resulting in zero velocity at the boundary.
Inlet/Outlet boundary condition
Inlet boundary condition specifies fluid properties entering a computational domain, while outlet condition describes fluid behavior exiting the domain. In ANSYS Fluent, inlet and outlet boundary conditions dictate how fluid enters and exits the simulation domain, ensuring mass conservation. You can specify velocity, pressure, or mass flow rate at both the inlet and outlet, depending on the flow scenario. These choices influence how the fluid behaves within the domain, and ANSYS Fluent might offer additional options for specifying turbulence, temperature, or other properties at these boundaries.
Symmetry boundary condition
The symmetry boundary condition assumes symmetry across a specified plane, reflecting flow properties symmetrically. It reduces computational domain size and enhances efficiency in fluid dynamics simulations.
Axisymmetric boundary conditions
Axisymmetric boundary conditions apply to cylindrical domains, assuming zero circumferential variation in the flow. This simplifies calculations by treating the system as 2D.
Click to access the Heat Transfer CFD
What are the boundary conditions in electromagnetics?
In electromagnetics, boundary conditions describe the behavior of electric and magnetic fields at the interfaces between different media or at the boundaries of a computational domain. These conditions are crucial for solving electromagnetic problems accurately. Here are some common types of boundary conditions in electromagnetics:
- Magnetic insulation boundary condition: The Magnetic Insulation boundary condition is used in electromagnetic simulations to represent a boundary where the magnetic field is assumed to be zero outside the domain.
- Magnetic field boundary condition: magnetic field boundary condition delineates how magnetic fields interact with boundaries. It’s crucial for simulating plasma behavior in fusion reactors or astrophysical phenomena. Various conditions, like perfect conductor or insulator, are used to model different materials’ responses to magnetic fields accurately.
- Electric insulation boundary conditions: This condition specifies that the normal component of the electric field is equal to zero.
- Electric field boundary conditions: Electric field boundary conditions dictate how the electric field behaves at the meeting point of two different materials.
- Impedance boundary conditions: It is utilized for situations where the electromagnetic field penetrates only a short distance outside the boundary. It approximates this penetration, thereby avoiding the need for including additional domains in the model, which can significantly simplify simulations. This condition is particularly useful in situations such as when modeling waveguides, antennas, or scattering problems, where the computational domain can be reduced without sacrificing accuracy.
- The Transition Boundary Condition: It is a specialized boundary condition used in electromagnetic simulations on interior boundaries. It effectively models a geometrically thin sheet of a medium that may not be electrically thin. TBCs account for the discontinuity in the tangential electric field across the sheet by relating it to the induced surface current density. This approach is particularly useful when the wave propagation is primarily in the normal direction to the thin layer.
What are boundary conditions in Finite Element and Finite Volume analysis?
Since both FEM and FVM are designed to solve differential equations, the types of boundary conditions used are the same as those for differential equations. However, in FEM and FVM, the boundaries are discretized along with the domain, and the boundary conditions are applied in this discrete environment.
Click to access the CFD Fluid Mechanics
What are boundary conditions in ANSYS Fluent?
ANSYS Fluent offers a variety of boundary conditions to accurately simulate fluid flow. Here, we examine the key boundary conditions related to fluid flow:
Velocity inlet boundary condition: This condition is used to specify the velocity and scalar properties of the flow, such as temperature, at inlet boundaries.
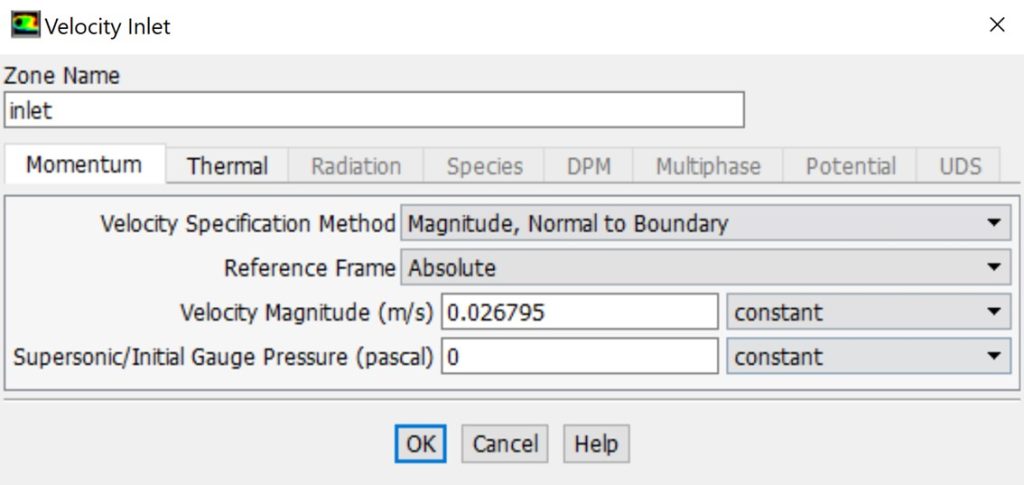
Velocity inlet boundary condition in ANSYS Fluent
Pressure inlet boundary condition: This condition is utilized to specify the total pressure and other scalar properties, such as temperature, at the flow inlets.
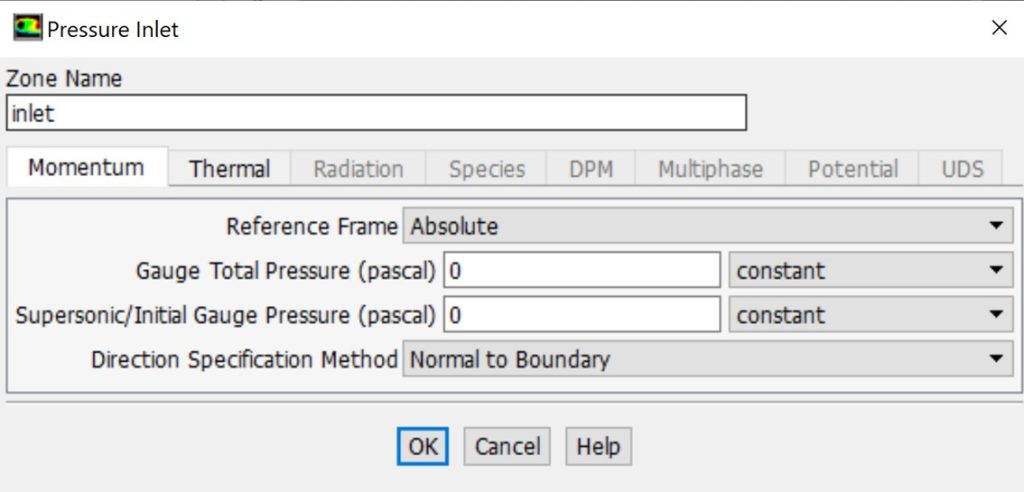
Pressure inlet boundary condition in ANSYS Fluent
Mass flow inlet boundary condition: In ANSYS Fluent, mass flow inlets set a specific mass flow rate for compressible flows. For incompressible flows, velocity inlets suffice since the constant density allows velocity to determine the mass flow.
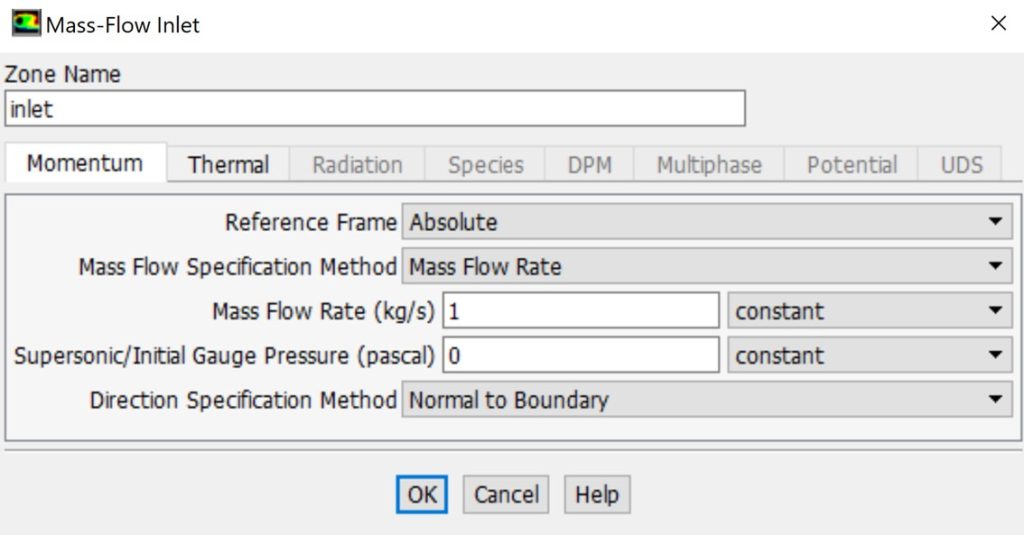
Mass flow inlet boundary condition in ANSYS Fluent
Pressure outlet boundary condition: It specify static pressure at outlets, aiding convergence during backflow, unlike outflow conditions.
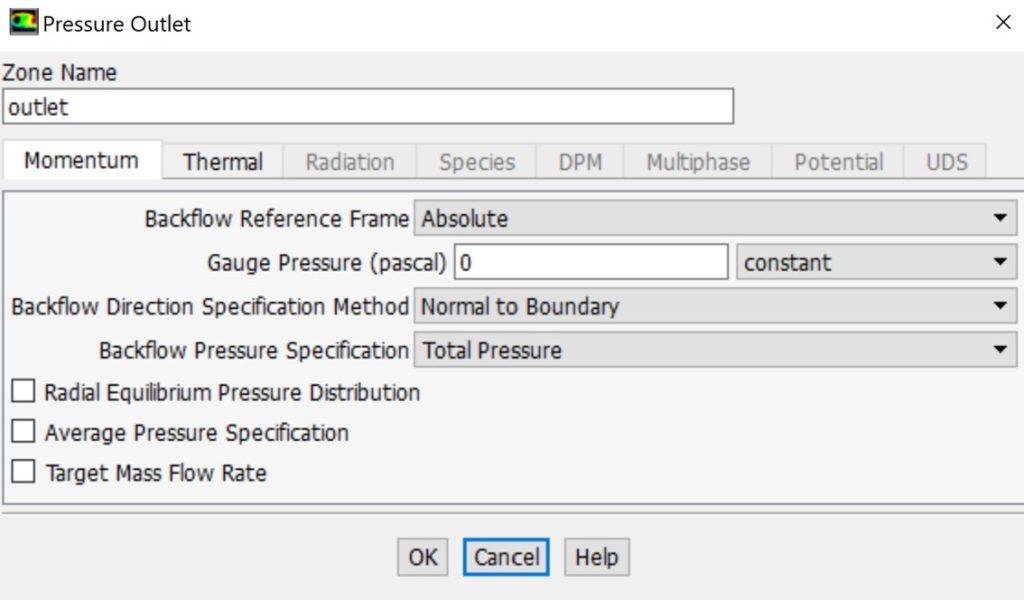
Pressure outlet boundary condition in ANSYS Fluent
Pressure far-field boundary condition: This boundary condition models free-stream compressible flow at infinity, specifying free-stream Mach number and static conditions, and is exclusively used for compressible flows.
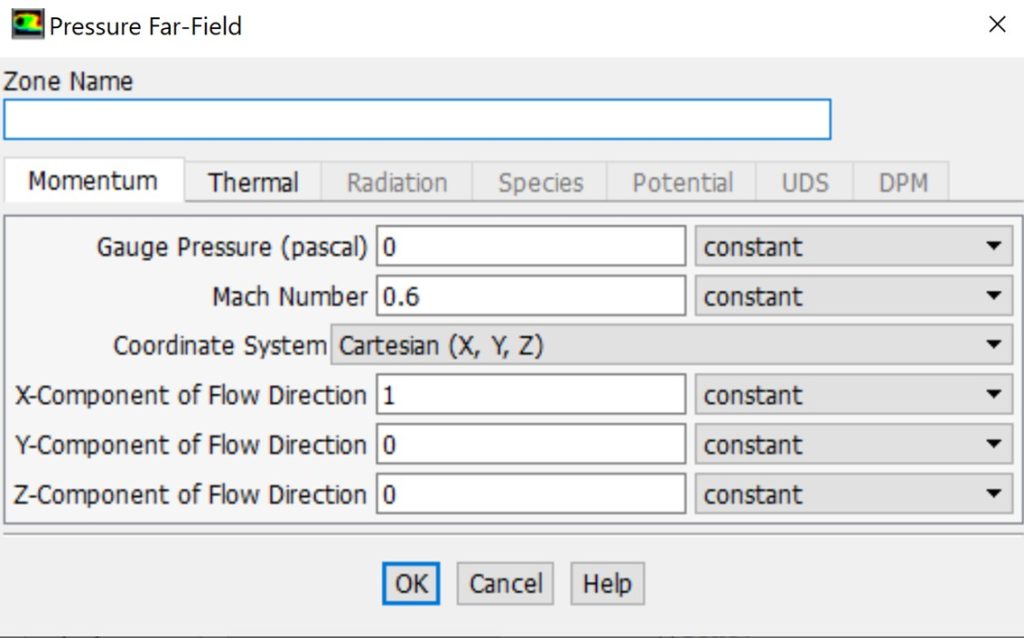
Pressure far-field boundary condition in ANSYS Fluent
Outflow boundary condition: This boundary condition simulates flow exits with unknown velocity and pressure, assuming zero streamwise gradient for flow variables (except pressure). They are suitable for fully developed flows but not for compressible flows.
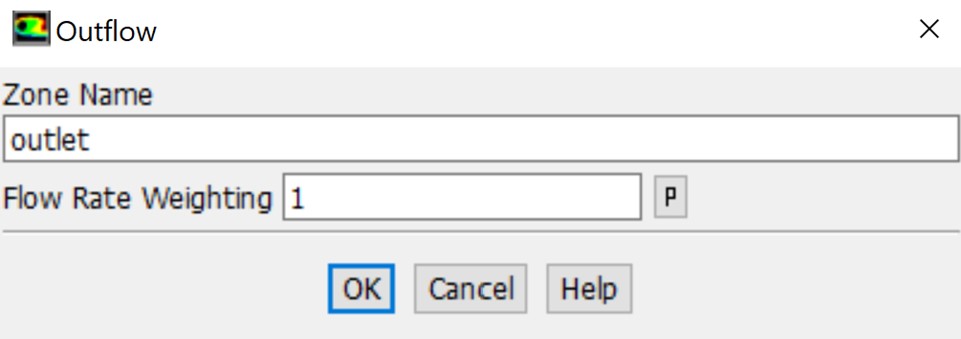
Outflow boundary condition in ANSYS Fluent
Inlet vent boundary condition: This boundary condition simulates specific characteristics of an inlet vent, including loss coefficient, flow direction, and ambient total pressure and temperature.
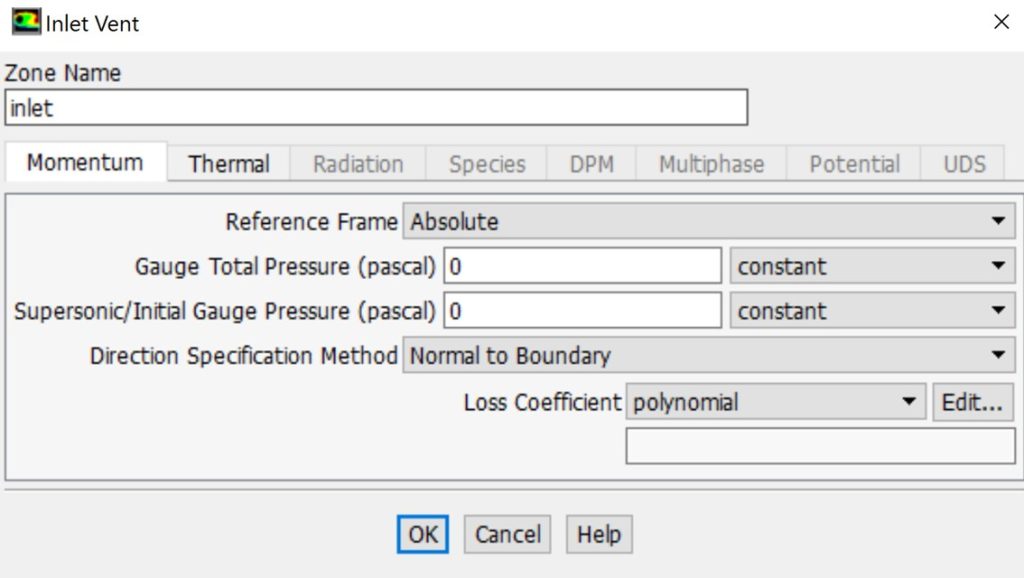
Inlet vent boundary condition in ANSYS Fluent
Intake fan boundary condition: This boundary condition models an external intake fan by incorporating a specified pressure jump, flow direction, and ambient total pressure and temperature.
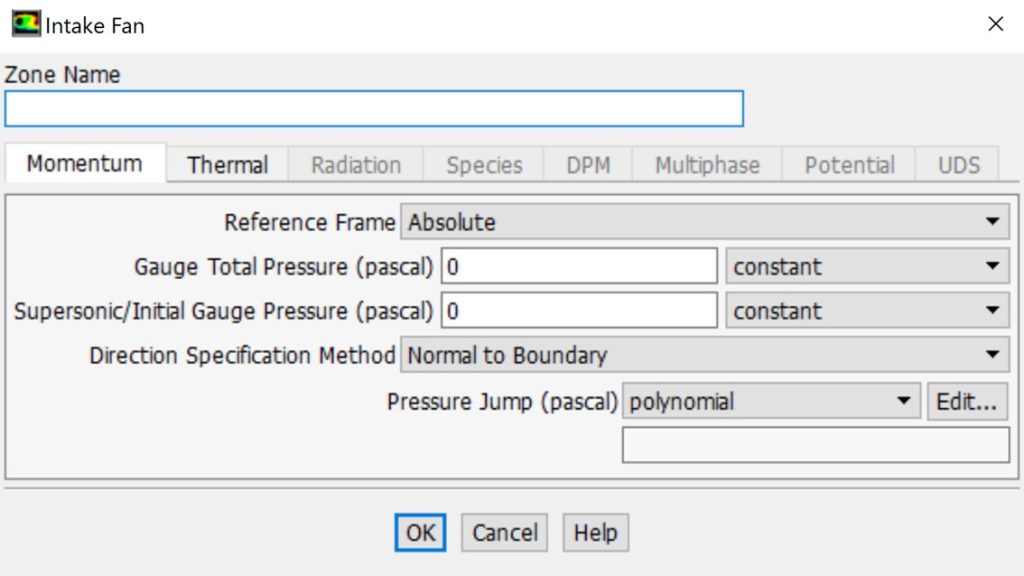
Intake fan boundary condition in ANSYS Fluent
Outlet vent boundary condition: This boundary condition simulates an outlet vent, considering a designated loss coefficient, and ambient static pressure and temperature at discharge.
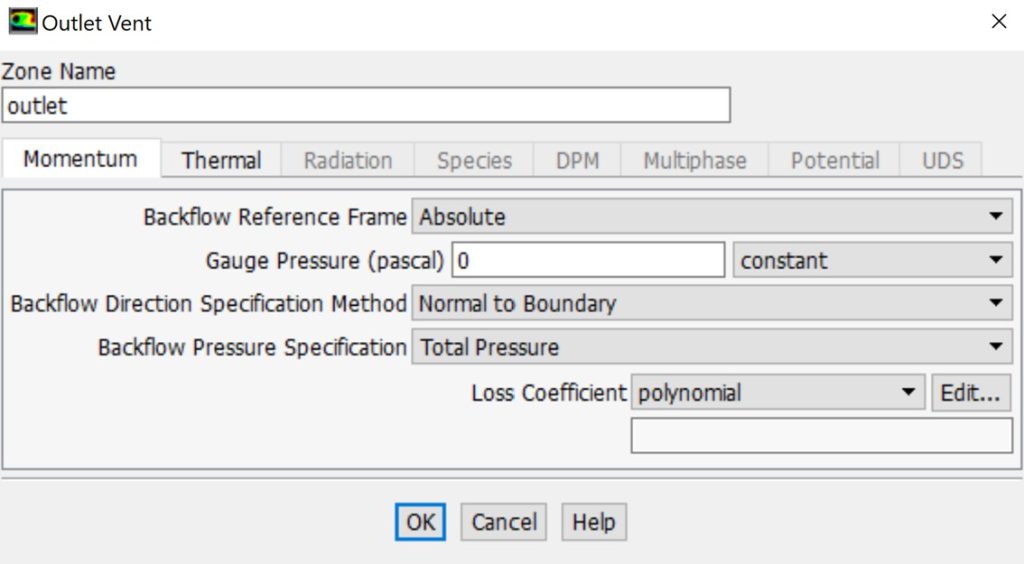
Outlet vent boundary condition in ANSYS Fluent
Exhaust fan boundary condition: This boundary condition simulates an external exhaust fan, accounting for a specified pressure jump and ambient static pressure at discharge.
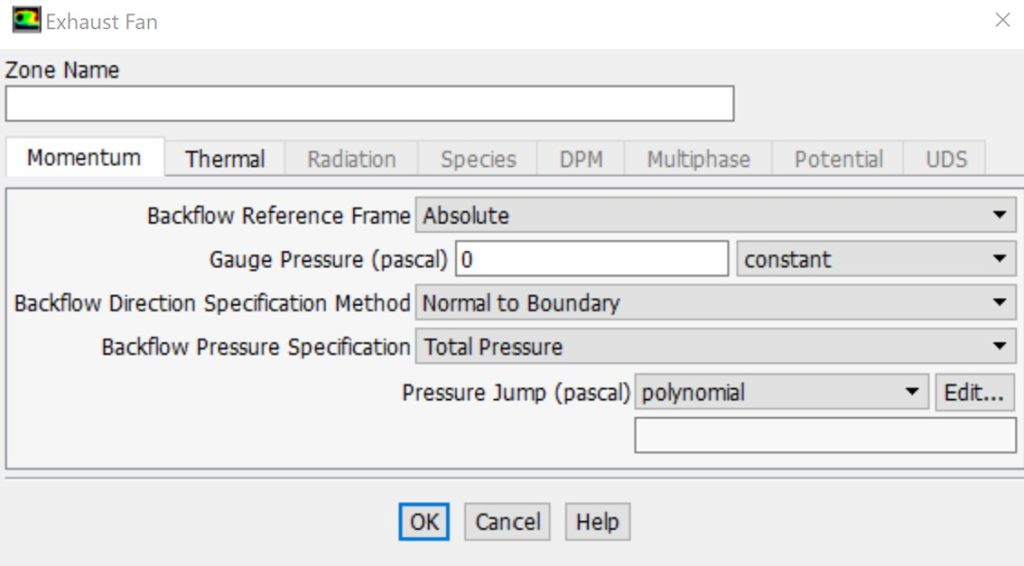
Exhaust fan boundary condition in ANSYS Fluent
Axis boundary condition: In ANSYS Fluent, the axis boundary condition models symmetry along an axis, reducing computational costs for systems exhibiting axial symmetry.
Symmetry boundary condition: this boundary condition reduces computational load by modeling symmetry along an axis.
Wall boundary condition: This boundary condition defines fluid-solid boundaries. By default, it enforces no-slip in viscous flows. Optionally, specify tangential velocity based on translational or rotational motion. “Slip” walls can be modeled by specifying shear.
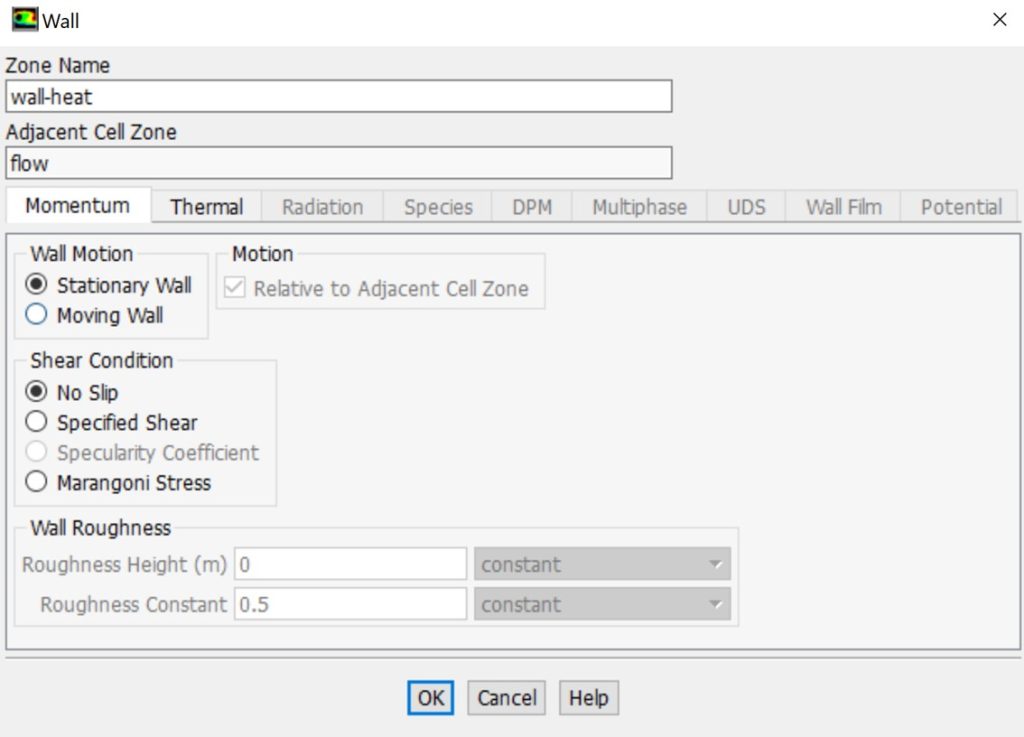
Wall boundary condition in ANSYS Fluent
Conclusion
In conclusion, boundary conditions serve as essential constraints in mathematical modeling, enabling the accurate representation of physical phenomena across diverse disciplines. From fluid dynamics to electromagnetics, understanding and appropriately applying boundary conditions are crucial for obtaining meaningful solutions to differential equations. By defining the behavior of systems at their edges, boundary conditions bridge theoretical frameworks with practical realities, facilitating robust simulations and analyses in scientific and engineering endeavors.

