Understanding the flow regime is crucial in CFD fluid mechanics. The Reynolds number (Re), a dimensionless quantity, helps determine whether a flow is laminar or turbulent, influencing various phenomena such as pressure drop, heat transfer, and friction factors. This article explores the significance of the Reynolds number, its applications, limitations, and its role in CFD simulations, providing insights into how it governs fluid behavior in different contexts.
What is Reynolds Number (Re) and its formula?
Scientists and engineers use the dimensionless Reynolds number to determine whether a flow is in a laminar or turbulent regime.
![\[ \mathrm{Re}=\frac{\rho V L}{\mu} \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-56044823b8aa2d6c08113a3a5d540044_l3.svg "Rendered by QuickLaTeX.com")
Where ρ [Kg.m-3] is the fluid density, V [m.s-1] is the characteristic velocity of the flow, L [m] is a characteristic length scale of the flow (e.g., pipe diameter for flow in a pipe) and μ [Pa.s] is the dynamic viscosity of the fluid. Another representation of the Re number is:
![\[ \mathrm{Re}=\frac{\rho V }{\nu} \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-30b27630a403c198f68a4ad17ea20762_l3.svg "Rendered by QuickLaTeX.com")
Where ν [m²/s] is kinematic viscosity.
In studying fluid flow inside a circular pipe experimentally, determining the transition from laminar to turbulent flow based solely on fluid velocity poses challenges if the laboratory fluid changes. To address this issue, dimensionless numbers come to the rescue. By understanding the variables influencing the phenomenon, such as fluid velocity, viscosity, and pipe diameter, the Reynolds number can be calculated. This number serves as a universal indicator, allowing predictions of flow regimes without the need for repeated experiments with varying fluids or scales.
The Reynolds number is expressed as a measure of the ratio of inertial force to viscous force. It should be noted that the Reynolds number is not the exact ratio of these two forces.
For more information about laminar and turbulent flow, see “The Differences Between Laminar and Turbulent Flow”
Significance of Reynolds number
In any phenomenon affected by flow regimes, the Reynolds number is important. It serves to describe and predict various phenomena. For example, convective heat transfer intensifies with turbulence growth, thus becoming a function of the Reynolds number. Additionally, dimensional analysis relies on this number. For instance, when testing a scaled ship model in the laboratory, insights gained from Reynolds and other dimensionless numbers help extrapolate the ship’s behavior to full dimensions.
Reynolds number limitations
Some of the limitations of Re number are:
• Transition Zone Ambiguity: The transition of the flow regime from laminar to turbulent does not occur suddenly, and a transitional zone is introduced to account for this gradual change. The behavior of this transitional zone is not clearly described by the Reynolds number alone.
• Dependency on Geometry: By altering the geometry, experimental tests need to be conducted again to ascertain the behavior of the fluid by Re number. For instance, the fluid behavior around a cylinder differs from that around a sphere at the same Reynolds number. Additionally, the characteristic length within the Reynolds number is defined differently for various geometries.
• Inapplicability to Complex Flows: In highly complex flows, such as those involving multiphase flows, non-Newtonian fluids, or turbulent boundary layers, the Reynolds number may not fully capture the intricacies of the flow behavior. Alternative dimensionless numbers or additional parameters may be required for accurate predictions.
• Simplifying Flow Behavior: The Reynolds number offers a simplified depiction of flow behavior, focusing solely on the ratio of inertial to viscous forces. However, it may neglect other influential factors such as turbulence intensity, boundary roughness, and compressibility effects.
Application of the Reynolds Number
The Reynolds number finds applications in a wide range of fields due to its ability to describe flow regimes and predict fluid behavior.
Here, we discuss three applications of the Reynolds number in fluid mechanics.
1. Fluid flow in a circular pipe:
The Reynolds number is vital for understanding fluid flow in a circular pipe. It predicts whether the flow will be laminar or turbulent, significantly influencing factors such as pressure drop and heat transfer. At Re < 2300, the flow is laminar; at 2300 < Re < 4000, the flow is transitional; and for Re > 4000, the flow is turbulent.
2. Boundary layer development on a flat plate:
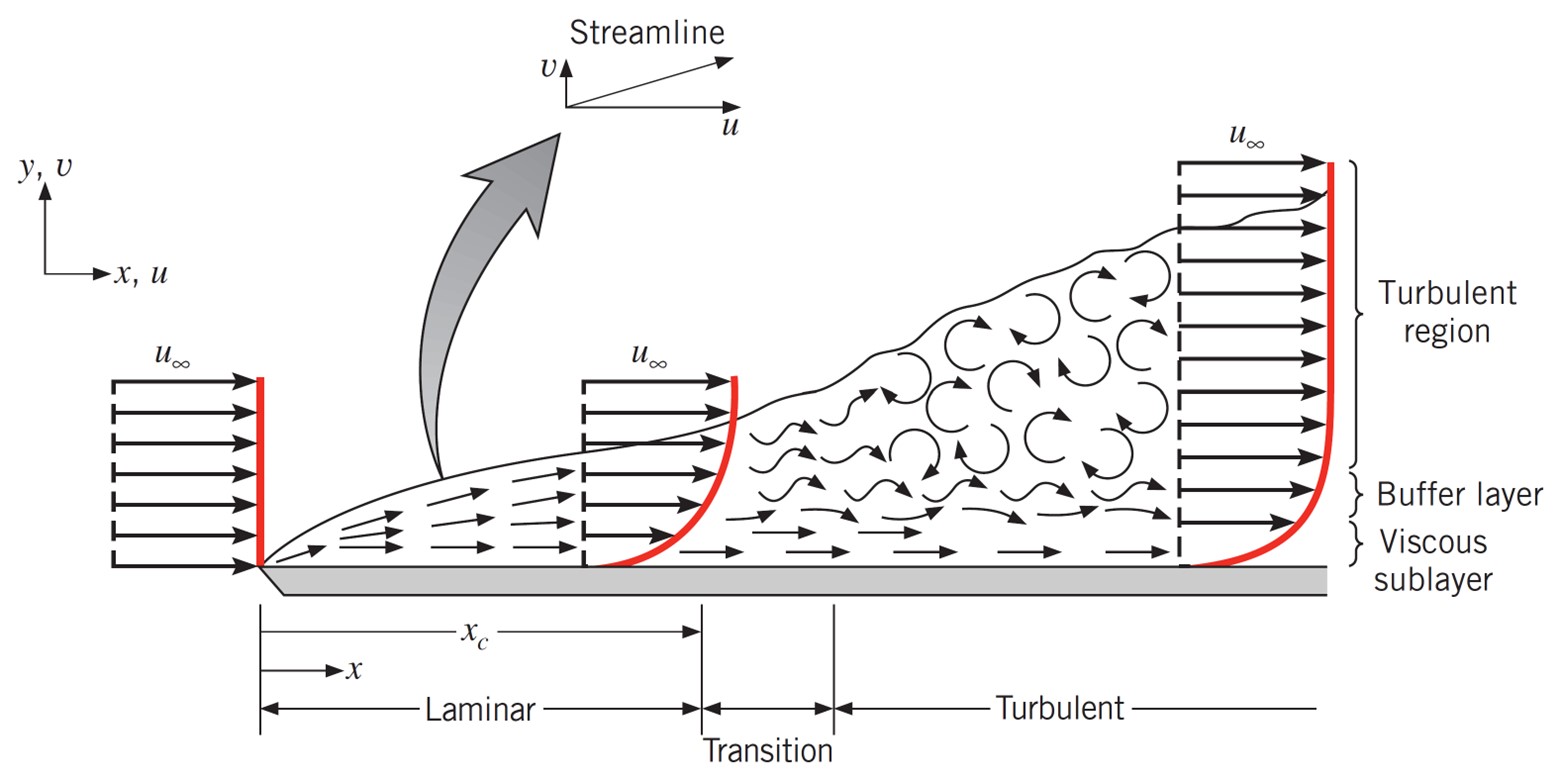
The development of a boundary layer on a flat plate is significantly influenced by the Reynolds number. As fluid flows over a flat plate, the region near the plate where the effects of viscosity are significant is called the boundary layer. This layer can be characterized by its flow regime, which is determined by the Reynolds number
To analyze the flow regime of the boundary layer on a flat plate, as illustrated in Figure 1, the distance x from the leading edge of the plate is used as the characteristic length scale, and the velocity of the fluid outside the boundary layer u∞ is used as the velocity in Equation 1 to calculate the Reynolds number.
As seen in Figure 1, the beginning of the flow regime change occurs at xc. The Reynolds number at this point is called the critical Reynolds number. In many sources, 105 has been introduced as the critical Reynolds number, but depending on surface roughness and the turbulence level of the free stream, this number can reach 3 × 106.
Figure 1. Velocity boundary layer development on a flat plate, from “Fundamentals of heat and mass transfer” by Frank P. Incropera et al.
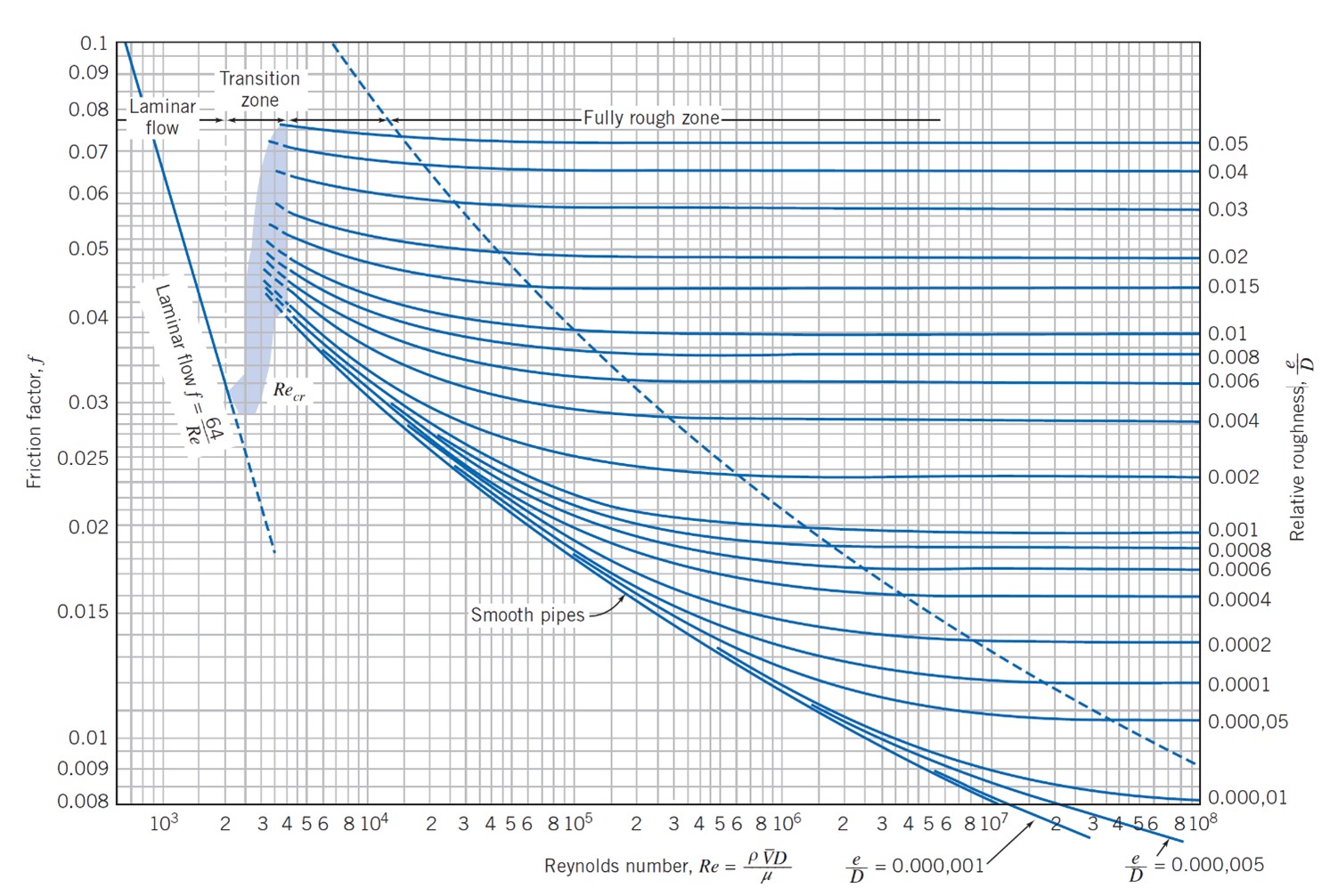
3. Friction Factor and Pressure Drop:
The friction factor f is a dimensionless quantity that reflects the energy loss due to friction between the flowing fluid and the pipe wall. A higher friction factor indicates a larger pressure drop along the pipe length. The friction factor is a function of Re number as can be seen in Figure 2. It should be noted that at high Reynolds numbers, the friction factor is primarily a function of relative roughness.
Figure 2. Friction factor for fully developed flow in circular pipes, from “Introduction to fluid mechanics” by Philip J. Pritchard et al.
What is Rayleigh number?
The natural convection flow regime, driven by temperature differences and buoyancy forces, is determined by the Rayleigh number (Ra), not the Reynolds number. It is defined as:
![\[ \mathrm{Ra}=\frac{g \beta \left( T_s - T_{\infty} \right) x^3 }{\nu \alpha} \]](https://cfdland.com/wp-content/ql-cache/quicklatex.com-9460c95c58ab745417f54795d612ef11_l3.svg "Rendered by QuickLaTeX.com")
The Rayleigh number (Ra) is defined with respect to various parameters: the acceleration due to gravity (g) in [m.s-2], the thermal expansion coefficient (β) in [1.K-1], the characteristic length scale (x) in [m], the thermal diffusivity (α) in [m2.s], the kinematic viscosity (ν) in square meters per second [m2.s], the surface temperature (TS) in [K], and the fluid temperature (T∞) in [K].
The Rayleigh number is proportional to the ratio of the buoyancy force to the viscosity, and it increases with the buoyancy force. However, this increase is not directly proportional; the Rayleigh number does not simply double when the buoyancy force is doubled.
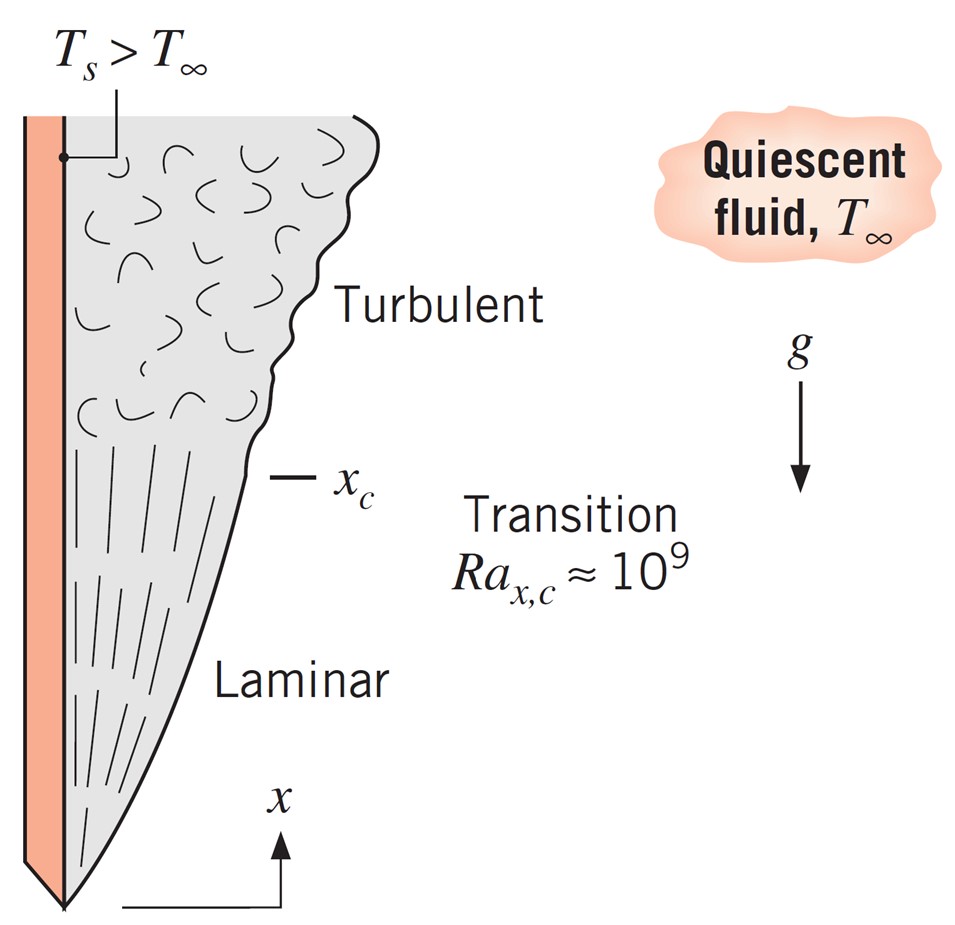
Figure 3. Free convection boundary layer transition on a vertical plate, from “Fundamentals of heat and mass transfer” by Frank P. Incropera et al.
In natural convection, the flow regime is determined by the Rayleigh number, not the Reynolds number. Figure 3 shows natural convection flow on a vertical plane. As can be seen, the flow regime changes at Ra = 109, which is called the critical Rayleigh number. Natural convection currents are created due to the temperature difference in the fluid, which causes a density difference and the resulting buoyancy force.
Why is Reynolds Number Important for CFD Analysis?
As stated so far, the flow regime affects the behavior of fluid phenomena, and determining the flow regime is very important for CFD simulations. Various software, such as ANSYS Fluent, do not directly calculate the Reynolds number or Rayleigh number. Instead, the Reynolds number or Rayleigh number is calculated outside of the software environment. Using external sources and experimental results, the flow regime corresponding to that Reynolds number (or Rayleigh number in the case of natural convection flow) is determined. Then, this information is applied in the ANSYS Fluent settings.
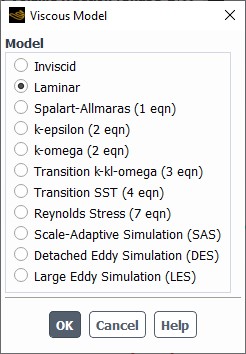
Under the title of “Viscous Models” in the software, all the simulation methods for the fluid flow regime available in the software are:
• Inviscid: In this model, it is assumed that fluid has no viscosity.
• Laminar: There is just one model for viscous laminar flows and it solves the ordinary Navier-Stokes equation. The following models are for simulating turbulent flow
• Spalart-Allmaras: It is a Reynolds-Averaged Navier-Stokes (RANS) model, suitable for aerodynamics applications.
• k-epsilon: It is a Reynolds-Averaged Navier-Stokes (RANS) model, suitable for general-purpose turbulence modeling in various applications.
• k-omega: It is a Reynolds-Averaged Navier-Stokes (RANS) model, suitable for modeling near-wall and low-Reynolds number turbulence.
• Transition k-kl-omega: It is a Reynolds-Averaged Navier-Stokes (RANS) model, suitable for modeling transitional flows from laminar to turbulent.
• Transition SST: This model is a combination of the k-epsilon and k-omega turbulence models.
• Reynolds Stress it is a RANS model suitable for simulating highly anisotropic turbulent flows.
• Scale-Adaptive simulation: A hybrid RANS-LES model suitable for resolving different turbulent scales.
• Detached Eddy Simulation: A hybrid RANS-LES model suitable for resolving eddies near walls.
• Large Eddy Simulation(LES): A method resolving large turbulent structures, suitable for high-resolution simulations. It is not a RANS model.
The details of each viscous model can be adjusted in the software. For example, for the k-epsilon model, there are three modes: standard, RNG, and realizable.
Figure 4. Viscous models, ANSYS Fluent
Reynolds number range
The Reynolds number starts from 0 and increases without any upper limit.
Reynolds number for turbulent flow
As seen in this article, the flow regime changes in different fluid phenomena at different Reynolds numbers, making it impossible to define a comprehensive Reynolds number at which the flow regime changes.
Conclusion
In conclusion, the Reynolds number serves as a fundamental parameter in fluid mechanics, guiding our understanding of flow regimes and predicting fluid behavior across diverse applications. While it simplifies flow analysis, its limitations underscore the need for supplementary parameters in complex flows. Despite this, the Reynolds number remains indispensable in engineering, providing valuable insights into fluid dynamics and facilitating the design and optimization of various systems and processes. Its ubiquity underscores its enduring significance in the field of fluid mechanics.