What is Reynolds Number (Re)?

shayan pakravan
Reading time: 10 min

The Reynolds number is one of the most important concepts in fluid mechanics and CFD. Named after Osborne Reynolds, this dimensionless number helps engineers predict flow patterns in different fluid flow situations. Understanding the Reynolds number equation is essential for anyone working with fluids, from designing pipes to analyzing aircraft performance.

Contents

Whether you’re studying laminar flow reynolds patterns or calculating turbulent reynolds number values, this guide will explain everything in simple terms. The Reynolds number tells us whether fluid flow will be smooth and orderly (laminar flow) or chaotic and mixed (turbulent flow).

Want to calculate Reynolds number quickly? Use our Reynolds Number Calculator for instant results without manual calculations.

Figure 1: Osborne Reynolds

In this comprehensive guide, we’ll explore:

The reynolds number formula and what each variable means
How to determine re number for laminar flow and reynolds number for turbulent flow
Practical applications in engineering and CFD simulation
Step-by-step calculation methods

Let’s start by understanding what exactly the Reynolds number is and why it matters so much in fluid dynamics.

What is Reynolds Number?

The Reynolds number (Re) is a dimensionless number used in fluid mechanics to predict flow patterns. It represents the ratio of inertial forces to viscous forces within a fluid. This simple ratio helps engineers understand whether a flow will be laminar or turbulent.

Think of it this way: when you pour honey (high viscosity), it flows smoothly in layers. But when you pour water (low viscosity) quickly, it splashes and swirls. The Reynolds number captures this behavior mathematically.

The Reynolds number equation helps us predict:

Whether flow will be smooth (laminar flow) or chaotic (turbulent flow)
How much mixing will occur in the fluid
The amount of friction and pressure drop in pipes
Heat and mass transfer rates

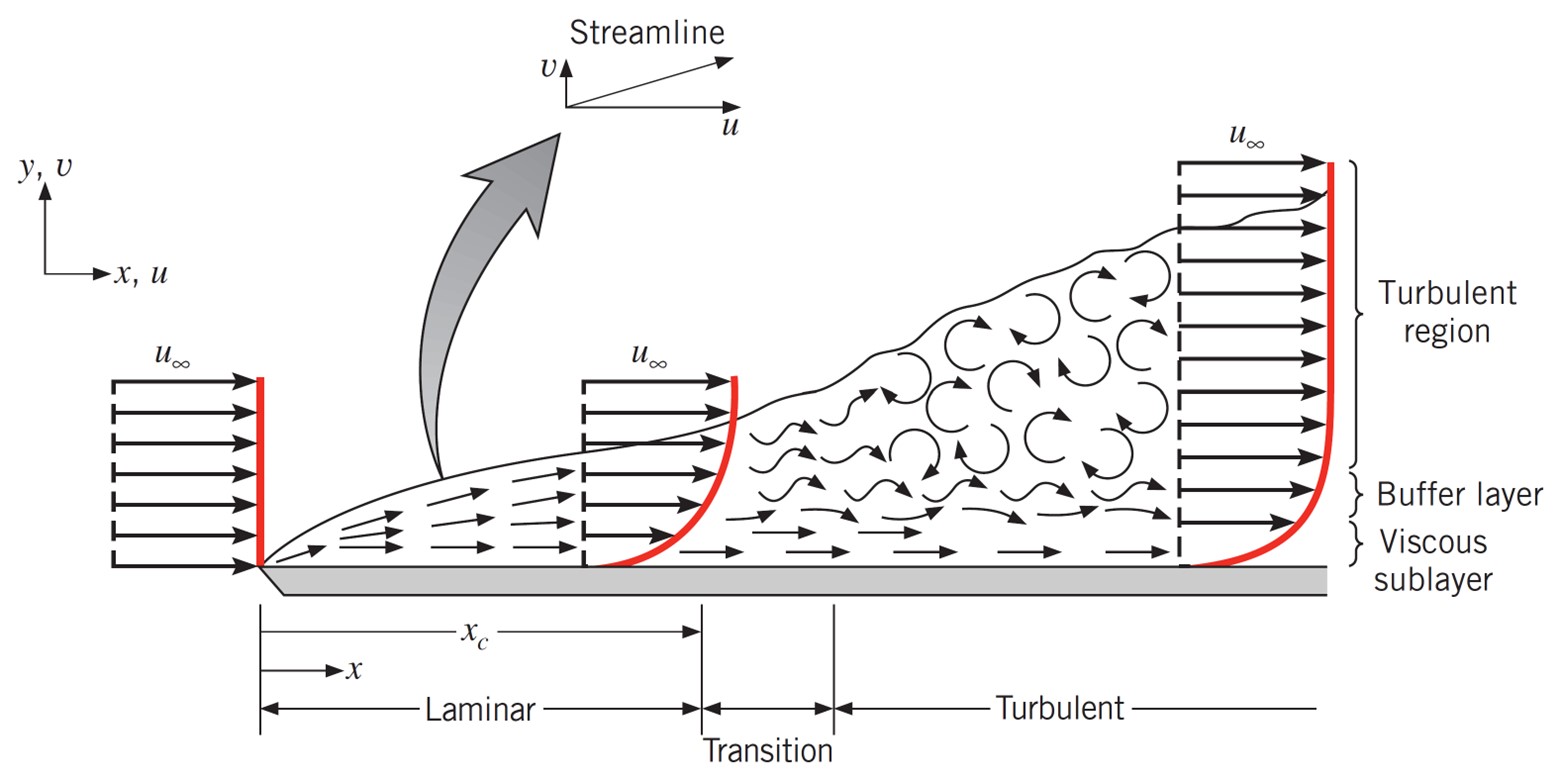
Figure 2. Velocity boundary layer development on a flat plate, from “Fundamentals of heat and mass transfer” by Frank P. Incropera et al.

Why is Reynolds Number Important?

The Reynolds number is crucial because it’s a universal predictor. Whether you’re designing a tiny blood vessel stent or a massive oil pipeline, the same Reynolds number principles apply. This makes it one of the most powerful tools in fluid dynamics.

Engineers use the Reynolds number to:

Design efficient piping systems
Optimize aircraft and vehicle aerodynamics
Predict weather patterns
Analyze blood flow in medical devices
Improve mixing in chemical reactors

The beauty of this dimensionless number is that it works for any fluid, any size, and any speed. That’s why understanding the reynolds number formula is essential for anyone working with fluids.

Reynolds Number Definition

The Reynolds number definition in simple terms: It is a dimensionless number that compares the relative importance of inertia forces to viscous forces in a flowing fluid.

$\mathrm{Re}=\frac{\rho V L}{\mu}$

Let’s break this down into simple parts:

Inertia forces: These try to keep the fluid moving in its current pattern
Viscous forces: These try to make the fluid stick together and flow smoothly
Dimensionless: The Reynolds number has no units – it’s just a pure number

The Reynolds number essentially answers this question: “Will this fluid flow in smooth layers or will it mix chaotically?”

Figure 3: Transition from laminar to turbulent regime with increase in Reynolds number

A simple analogy: Imagine walking slowly through a swimming pool (low Reynolds number) – the water flows smoothly around you. Now imagine running through the pool (high Reynolds number) – the water splashes and creates turbulence.

This dimensionless number was introduced by Osborne Reynolds in 1883. He discovered that the transition from laminar flow to turbulent flow always occurred at similar Reynolds number values, regardless of the pipe size or fluid type.

The Reynolds number symbol is Re (sometimes written as NRe), named in honor of Osborne Reynolds.

Reynolds Number Formula and Equation

The Reynolds number equation is one of the most fundamental formulas in fluid mechanics. Here’s the standard Reynolds number formula:

$\mathrm{Re}=\frac{\rho V D}{\mu}$

Where:

Re = Reynolds number (dimensionless)
ρ (rho) = Fluid density (kg/m³)
V = Characteristic velocity of the fluid (m/s)
D = Characteristic length or diameter (m)
μ (mu) = Dynamic viscosity of the fluid (Pa·s or N·s/m²)

The Reynolds number formula can also be written using kinematic viscosity:

$\mathrm{Re}=\frac{\rho V }{\nu}$

Where:

ν (nu) = Kinematic viscosity (m²/s)
ν = μ/ρ (kinematic viscosity equals dynamic viscosity divided by density)

Both forms of the Reynolds number equation give the same result. Engineers choose which formula to use based on the available data.

Let’s understand what each part of the reynolds number formula means:

Velocity (V): The speed of the fluid flow. Higher velocity means higher Reynolds number.
Characteristic Length (D):
- For pipes: Use the pipe diameter
- For non-circular ducts: Use the hydraulic diameter
- For flow over flat plates: Use the distance from the leading edge
- For flow around objects: Use the object’s characteristic dimension
Density (ρ): How heavy the fluid is per unit volume. Water has higher density than air.
Viscosity (μ): The fluid’s resistance to flow. Honey has high viscosity, while water has low viscosity.

The Reynolds number equation tells us that:

Larger pipes, faster flows, and denser fluids increase Re
More viscous fluids decrease Re

How to Calculate Reynolds Number

Now that you know the Reynolds number formula, let’s look at how to calculate Reynolds number for your specific problem. The process is straightforward and involves a few simple steps.

Find Your Fluid Properties: First, you need to know the density (ρ) and viscosity (μ) of your fluid at its operating temperature. You can find these values in engineering handbooks or online tables for common fluids like water or air.
Determine the Flow Velocity (V): Next, you need the average speed of the fluid. For example, the speed of water flowing through a pipe.
Measure the Characteristic Length (D): This is the most important dimension for your flow. For pipe flow, it’s the inner diameter of the pipe.
Ensure Consistent Units: It is very important that all your values use a consistent unit system, like the SI system (meters, kilograms, seconds). Mismatched units are a common source of error.

The Easiest Way to Calculate Reynolds Number

Manually calculating the Reynolds number can be tricky, and it’s easy to make mistakes with units. For a fast, easy, and accurate calculation, we strongly recommend using our online tool.

Save time and avoid errors! Visit our Reynolds Number Calculator to get instant results. Just enter your values, and our tool will do the rest. This is the best way to ensure you have the correct Reynolds number for your analysis.

Reynolds Number Ranges: Laminar vs Turbulent Flow

The most practical use of the Reynolds number is to predict the flow regime. Based on its value, we can classify the flow as laminar, transitional, or turbulent.

For flow inside a pipe, the generally accepted ranges are:

Laminar Flow (Re < 2300): The re number for laminar flow is low. This means the flow is smooth, orderly, and moves in parallel layers.
Transitional Flow (2300 < Re < 4000): This is the reynolds number transition range where the flow is unstable and can change between laminar and turbulent.
Turbulent Flow (Re > 4000): A high reynolds number for turbulent flow indicates a chaotic, swirling flow with significant mixing. Most industrial applications involve a turbulent reynolds number.

Understanding the characteristics of each flow type is critical. For a detailed comparison, visual examples, and a complete explanation of the physics, please read our comprehensive article:

Reynolds Number in CFD and ANSYS Fluent

The Reynolds number is fundamental to CFD (Computational Fluid Dynamics) and software like ANSYS Fluent. Before running any simulation, engineers must calculate the Reynolds number to set up the model correctly.

Why is Reynolds Number Critical for CFD?

The Reynolds number in CFD determines which turbulence model you should use.

For a low re number for laminar flow, you can use the Laminar model in ANSYS Fluent. This model is simple and computationally fast.
For a high turbulent reynolds number, you must select a turbulence model (like k-epsilon or k-omega). These models are designed to capture the chaotic effects of turbulent flow.

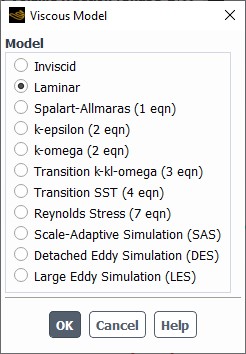
Figure 4. Viscous models, ANSYS Fluent

Choosing the wrong model based on an incorrect Reynolds number will lead to inaccurate simulation results. For example, using a laminar model for a highly turbulent flow will fail to predict mixing and pressure drop correctly.

In ANSYS Fluent, you don’t input the Reynolds number directly. Instead, you define:

Fluid Properties: Density and viscosity in the Materials panel.
Flow Velocity: At the inlet boundary condition.
Geometry Dimensions: In your CAD or SpaceClaim model.

ANSYS Fluent uses these inputs to solve the governing equations for that specific Reynolds number condition. The Reynolds number helps you, the engineer, to validate the simulation setup and understand the expected flow behavior.

Application of the Reynolds Number

The Reynolds number finds applications in a wide range of fields due to its ability to describe flow regimes and predict fluid behavior.

Here, we discuss three applications of the Reynolds number in fluid mechanics.

1. Fluid flow in a circular pipe:

The Reynolds number is vital for understanding fluid flow in a circular pipe. It predicts whether the flow will be laminar or turbulent, significantly influencing factors such as pressure drop and heat transfer. At Re < 2300, the flow is laminar; at 2300 < Re < 4000, the flow is transitional; and for Re > 4000, the flow is turbulent.

2. Boundary layer development on a flat plate:

The development of a boundary layer on a flat plate is significantly influenced by the Reynolds number. As fluid flows over a flat plate, the region near the plate where the effects of viscosity are significant is called the boundary layer. This layer can be characterized by its flow regime, which is determined by the Reynolds number

To analyze the flow regime of the boundary layer on a flat plate, as illustrated in Figure 1, the distance x from the leading edge of the plate is used as the characteristic length scale, and the velocity of the fluid outside the boundary layer u∞ is used as the velocity in Equation 1 to calculate the Reynolds number.

As seen in Figure 1, the beginning of the flow regime change occurs at x_c. The Reynolds number at this point is called the critical Reynolds number. In many sources, 10⁵ has been introduced as the critical Reynolds number, but depending on surface roughness and the turbulence level of the free stream, this number can reach 3 × 10⁶.

3. Friction Factor and Pressure Drop:

The friction factor f is a dimensionless quantity that reflects the energy loss due to friction between the flowing fluid and the pipe wall. A higher friction factor indicates a larger pressure drop along the pipe length. The friction factor is a function of Re number as can be seen in Figure 2. It should be noted that at high Reynolds numbers, the friction factor is primarily a function of relative roughness.

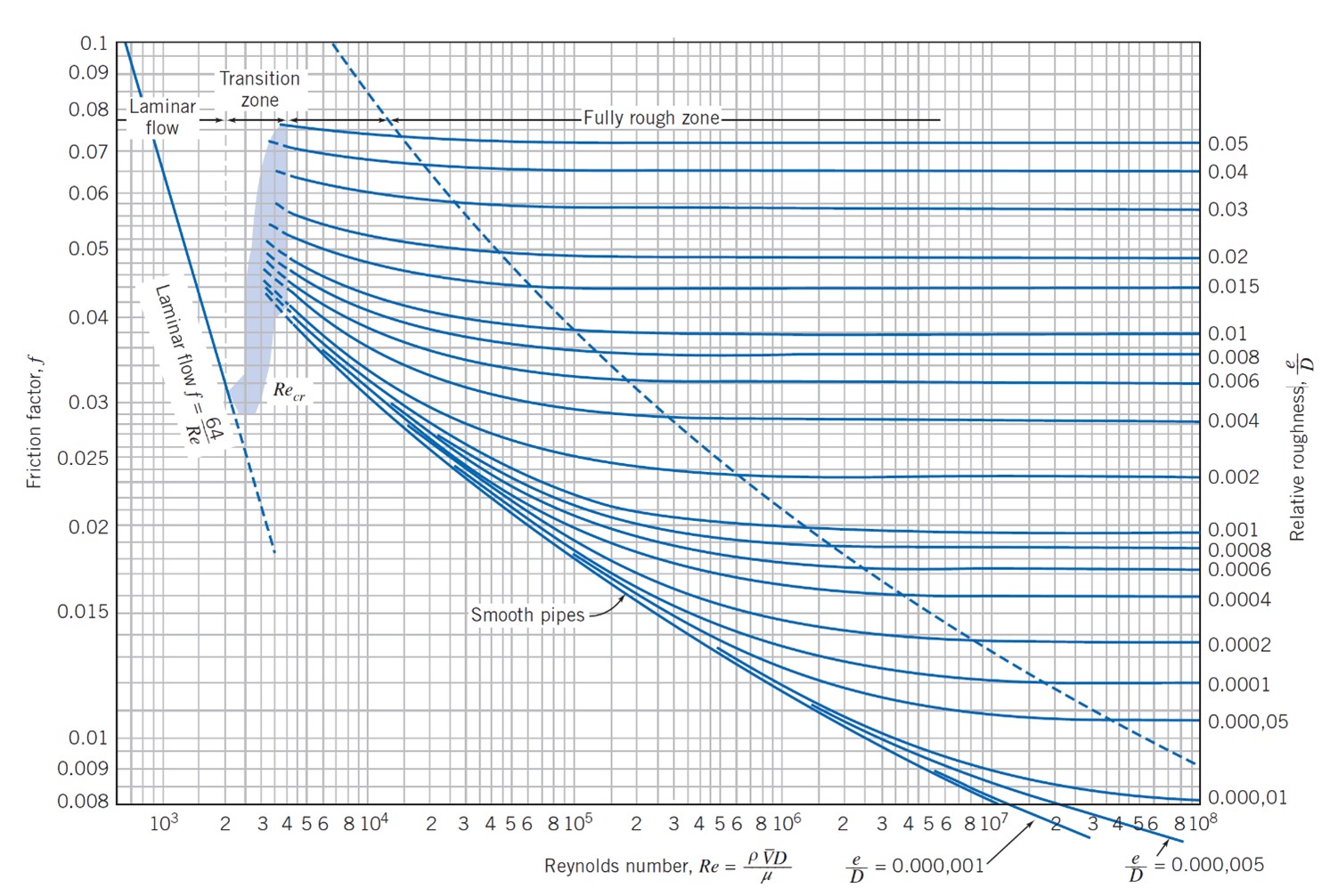
Figure 5. Friction factor for fully developed flow in circular pipes, from “Introduction to fluid mechanics” by Philip J. Pritchard et al.

Conclusion

The Reynolds number is a powerful and essential tool in fluid mechanics and CFD. This simple dimensionless number gives us deep insight into a fluid’s behavior, allowing us to predict whether a flow will be smooth and laminar or chaotic and turbulent.

From understanding the basic reynolds number definition to applying the reynolds number formula, you now have the knowledge to analyze fluid flow problems more effectively. We learned that the Reynolds number equation is a ratio of inertial forces to viscous forces, which is a key concept in predicting flow transitions.

Remember these key takeaways:

A low Reynolds number (e.g., Re < 2300 in pipes) signifies laminar flow.
A high Reynolds number (e.g., Re > 4000 in pipes) signifies turbulent flow.
In CFD simulations with tools like ANSYS Fluent, calculating the Reynolds number is the first step to choosing the correct physical model.

For quick and accurate calculations, don’t forget to use our powerful Reynolds Number Calculator. It’s the easiest way to find the Re for your specific application.