Introduction to DPM Breakup Models

A critical aspect of droplet`s breakup during DPM CFD simulations is the breakup process, which is fundamental to understanding spray and atomization phenomena. In this blog, a brief explanation of spray and atomization breakup will be given. After that, six breakup models provided in ANSYS Fluent will be practically discussed. These concepts are essential for optimizing industrial applications such as fuel injection, mist spray systems, agricultural spraying, etc.

 

DPM Breakup Concepts: Atomization Regimes

Generally, the atomization regimes can be categorized into:

Primary breakup (Jet breakup):

It consists of three regimes:

1. Rayleigh:
2. First wind-induced
3. Second wind-induced

These regimes describe the continuous disintegration of a liquid jet as it pinches off from a nozzle. The Rayleigh regime, as illustrated in Figure 1, shows the initial stages of jet breakup. In this stage, surface tension forces dominate the aerodynamic forces (such as drag – read dpm drag law models for more info). As a result, the liquid jet breaks into large distinct droplets. However, this early stage will be substituted by wind-induced regimes because the aerodynamic forces take the lead. This transmission results in more chaotic and unorganized breakup pattern. As time goes by, the atomization regime, which is considered part of the secondary breakup process takes place.

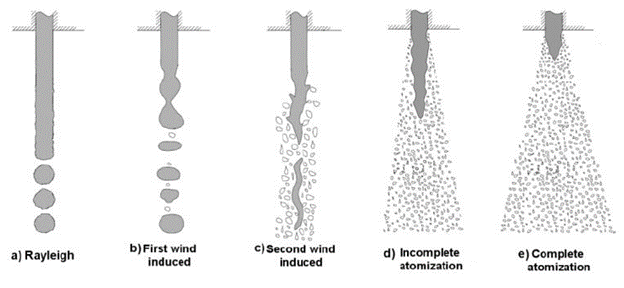
Figure 1: Atomization regimes in primary breakup – Reference DOI: https://doi.org/10.1615/AtomizSpr.2012004051

 

Secondary breakup (Droplet breakup)

Extra forces are needed to destroy the central sheet and ligaments and separated droplets for transmission from primary breakup to the secondary stage. Hydraulic instabilities and body forces such as acceleration are the keys to fully developed spray and atomization. The Weber number (We) plays a leading role in determining the breakup behavior. This dimensionless parameter represents the ratio of deforming inertial forces to cohesive forces.

   

We = Weber number

ρ = fluid density

u = velocity of the fluid

L = characteristic length (e.g., diameter of a droplet or jet)

σ = surface tension of the fluid

A higher Weber number means lower surface tension or higher aerodynamic forces. In other words, the higher the Weber number, the faster transmission from the Rayleigh regime to complete atomization.

 

DPM Break-up models

In ANSYS Fluent, six breakup models are described, including TAB, Wave, KHRT, SSD, Madabhushi, Schemehi. You are supposed to enable breakup in the physical models panel along with Unsteady particle tracking first. Then, in Set injection panel ==> Physical Models tab, you can see Breakup sub-section (see Fig. 2). (If you want to read more about DPM physical models, check dpm physical model blog).

 

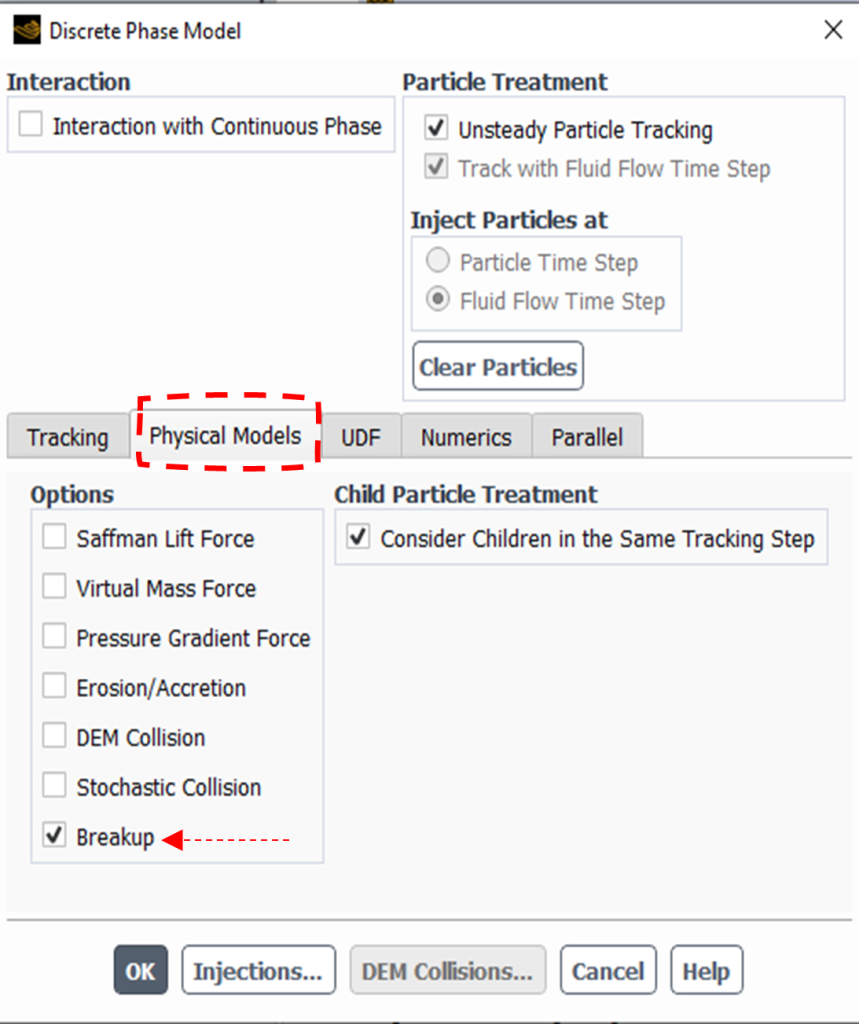
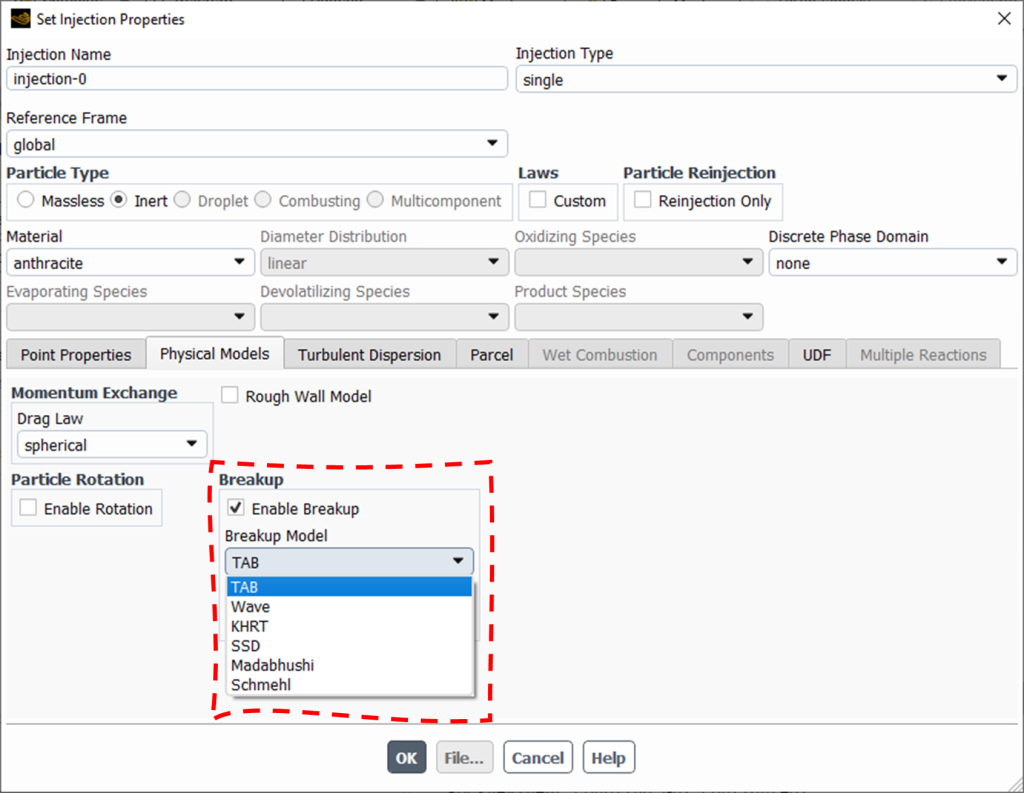
Figure 2: DPM breakup models in ANSYS Fluent: step 1: enable breakup sub-model – step2: find breakup models in injection box

 

*** Each breakup model has a complex theoretical background, which can be found in ANSYS Theory Guide. This article adopted a practical approach and only focused on pivotal information about the application and necessary fundamentals ***

 

1) TAB Breakup Model (Taylor Analogy Breakup)

The Taylor Analogy Breakup (TAB) model, as its name suggests, relies on Taylor’s analogy between an oscillating droplet and a spring-mass system to predict droplet behavior. It is mostly applicable in evaporating spray systems and low-speed sprays (We<100).

Generally, in TAB model, the spring-mass system relates to a distorting and oscillating droplet by the following analogous components:

Restoring force of spring ==> Surface tension forces

External force ==> Droplet drag force

Damping force ==> Droplet viscosity forces

The analogy once again proves the importance of knowing drag laws in DPM concepts.

Avoiding the governing equations, the droplet breakup in this model occurs when the distortion exceeds a critical ratio of the droplet radius, typically set at:

   

Where:

x is the Horizontal distortion of the droplet from a spherical state

Cb is the constant value equal to 0.5

r is spherical droplet radius

In order to employ TAB breakup model in ANSYS Fluent, the software asks for specifying two factors (see Fig. 3):

• Y0: Representing the initial distortion at time zero. Increasing y0 means faster breakup ==> Smaller droplet diameter ==> Shorter penetration length (due to drag force)
• Breakup Parcels: This parameter represents the sum of parent and child parcels during a breakup event.

Figure 3: TAB breakup model in ANSYS Fluent

For instance, Figure 4 illustrates a scenario where 3 parcels are injected. If the Breakup Parcel parameter is set to 4, each parent parcel produces 3 child parcels, resulting in a total of 12 parcels (3 parents, and 9 children).

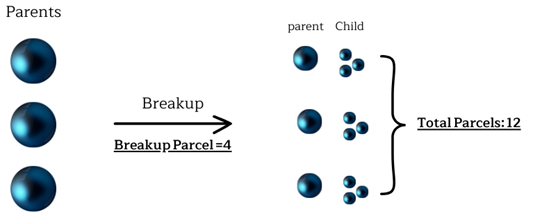
Figure 4: Parent and Child parcels after breakup under TAB model

 

2) Wave Breakup Model

The Wave Breakup Model, developed by Reitz, is a wise choice for simulating droplet breakup in high-Weber-number flows (We>100). Inaccurately said in some references, it serves as an alternative to the TAB (Taylor Analogy Breakup) breakup model. Fundamentally, Wave breakup model assumes that droplet breakup is induced by the relative velocity between gas and liquid phases and adopt jet stability analysis to predict breakup time and produced droplet sizes.

At its core, the Wave Breakup Model employs a mathematical formulation based on the Kelvin-Helmholtz instability theory. The model accumulates mass from the parent drop at a rate given by:

   

Where:

m_p is the mass of the parent drop

m_s is the mass of the stable drop size

and τ is the breakup time

This process continues until the shed mass equals 5% of the initial parcel mass, at which point a new parcel is created. Then, the radius of the new droplet is determined by:

   

Where:

B_0 is a model constant (typically 0.61, default in ANSYS Fluent)

Λ represents the wavelength of the fastest-growing instability on the liquid surface

Now, let`s check the parameters ANSYS asks from the user to define when using Wave breakup model (see Fig. 5).

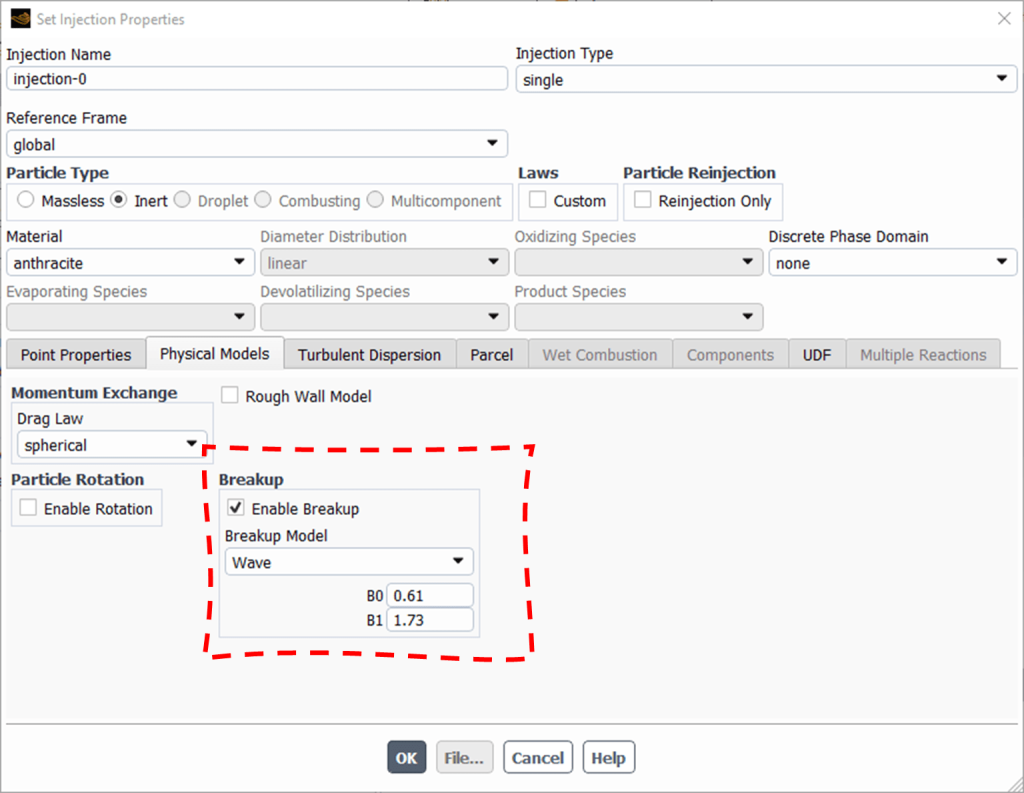
Figure 5: B0 & B1 parameters in Wave Breakup Model in ANSYS Fluent

• B_0 (usually 0.61): Influences drop size
• B_1: The breakup time constant, determining mass loss rate

Tip: A larger B_1 value means slower mass loss and less intense gas-liquid interaction. According to ANSYS guide, it is recommended to be between 15-60.

Tip: Larger B_1 ==> Larger droplet size ==> Longer Penetration Length

 

3) Kelvin-Helmholtz / Rayleigh-Taylor (KHRT) Breakup Model

The KHRT (Kelvin-Helmholtz Rayleigh-Taylor) Breakup Model, as its name says, combines two distinct physical mechanisms to predict droplet breakup:

• Kelvin-Helmholtz waves driven by aerodynamic forces
• Rayleigh-Taylor instabilities due to the acceleration of shed drops

This model tracks wave growth on the droplet surface like the Wave breakup model, with breakup occurring due to the fastest-growing instability based on local conditions.

The KHRT model assumes the liquid core is near the nozzle region, and child droplets are shed from the liquid core because of abrupt acceleration during injection to the freestream. The liquid core approximation follows a concept called “blobs” which you can read more about in references, see Fig. 6.  The length of this core is calculated using the following equation:

   

Where:

L is the liquid core length

CL is the Levich constant

d0 is a reference nozzle diameter

ρl and ρg are the liquid and gas densities, respectively

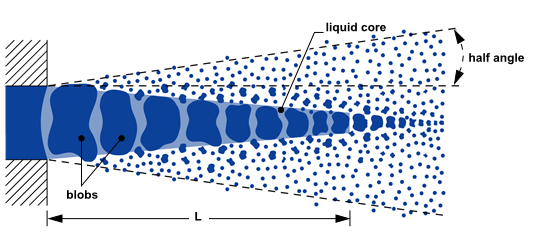
Figure 6: KHRT model and liquid core near nozzle region with blobs approximation – adopted from ANSYS Help

So the question is when to use KHRT model?

Knowing the fundamentals of the KHRT model makes it more understandable where to use it. To conclude, KHRT model is handy for simulating high-weber-number & High-pressure sprays and injections. Based on the literature, KHRT model can be employed where Catastrophic Breakup is expected, see Fig. 7.

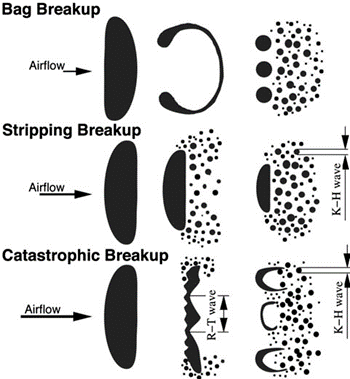
Figure 7: KHRT breakup model and catastrophic breakup – DOI:10.1007/978-1-4419-7264-4_9

To put KHRT breakup model into use in ANSYS Fluent, the software asks for specifying five parameters (Fig. 8): B0, B1, C_L, C_TAU, and C_RT. These parameters are divided into two categories:

• Wave (KH) Model Constants:
• B0: This parameter has a default value of 0.61. It influences the initial conditions of the liquid jet and its stability.
• B1: The recommended range for B1 is 15-60. Importantly, a larger B1 value will delay the Kelvin-Helmholtz (KH) breakup. So it allows users to control the timing of the primary breakup process.
• RT Model Constants:
• CL: This is the Levich model constant. A larger CL value indicates a longer breakup length, affecting how far the initial breakup occurs from the nozzle.
• Ctau: This is the breakup time constant. It determines how fast the breakup process occurs.
• CRT: This parameter is used to determine the criteria and time required for Rayleigh-Taylor (RT) breakup. Notably: A smaller CRT value will make the RT breakup process faster. It also produce smaller droplets.

Figure 8: KHRT breakup model in ANSYS fluent

Tip: The KHRT model results in a lower penetration length than compared to the wave breakup model.

 

4) Stochastic Secondary Droplet (SSD) Breakup Model

high Weber number sprays under diesel and gas turbine conditions.

Unlike models such as Wave and TAB, which use a single-diameter scale, the SSD model treats droplet breakup as a discrete random event. To some extent, this approach brings uneven distribution of diameter scales over a range, resulting in a more realistic simulation of the breakup process. Moreover, breakup probability is not dependent on parent droplet size in SSD breakup model. As the model`s name refers to (Stochastic Secondary Droplet), the secondary droplet size is sampled from an analytical solution (Fokker-Planck equation).

To adopt proper parameters

As usual, we are not exploring the theoretical formulas of the model. However, it is essential to comprehend the following governing equations to utilize the model properly:

   

Where:

Wecr is the critical Weber number

σl is the surface tension

ρg is the gas density

urel is the relative velocity

and also:

   

Where:

B is the breakup constant

ρl is the liquid density

r is the droplet radius

Tip: The Breakup subjects to droplets larger than the critical radius (Step 1). When a droplet’s breakup time exceeds the critical breakup time, a breakup occurs (Step 2).

Now look at Fig. 9 to see what ANSYS inputs are when SSD breakup model is enabled.

• Critical We: The default value is 6. Consequently, the software uses the critical We to calculate the critical radius.
• Core B1: This user-specified constant defines the breakup time. The default value is 1.73.
• Xi: A negative dimensionless parameter that determines how much the child particles are smaller than the original parcel.
• Target NP controls the number of parcels created during a breakup event, which affects statistical error and computational costs. Although there’s a default limit of 50 parcels per breakup event, the actual number of drops per parcel may sometimes deviate from the target NP. In other words, the target NP represents the average NP.

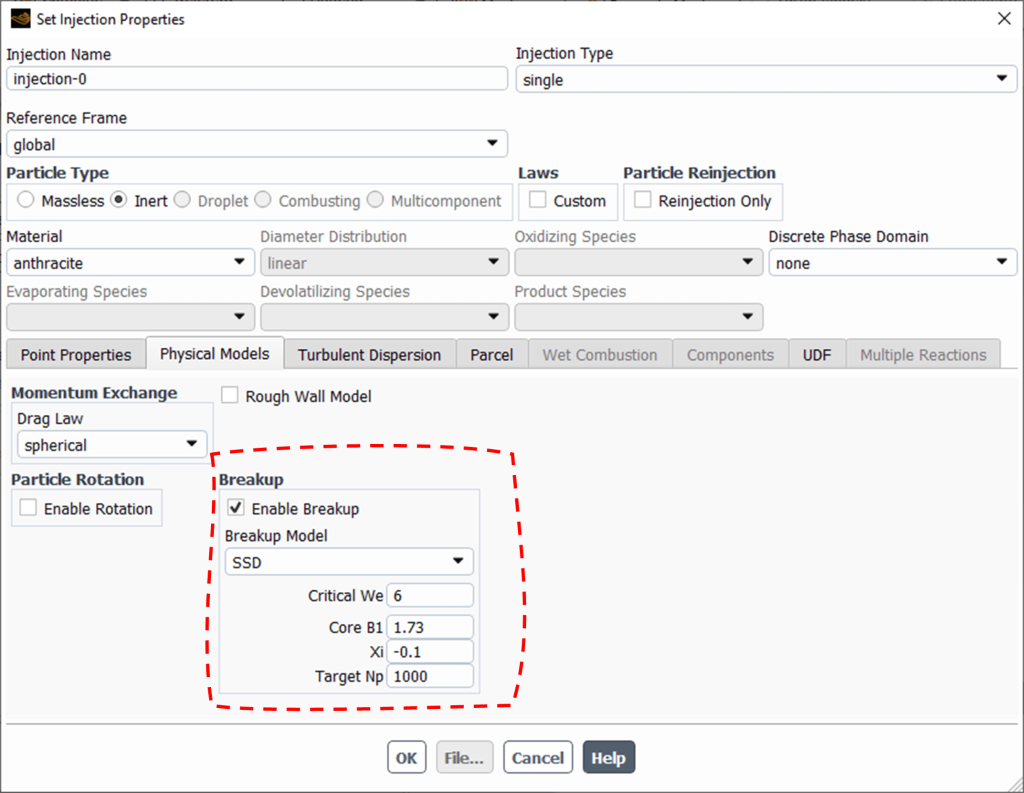
Figure 9: SSD breakup model parameters in ANSYS Fluent

 

5) Madabhushi Breakup Model

As discussed in the introduction of the present blog, when a liquid is injected into a gas, it typically undergoes two stages of breakup: Primary Breakup & Secondary Breakup. The Madabhushi breakup model addresses the drawbacks of traditional models:

• Primary Breakup: Madabhushi model uses the Wave breakup model to simulate the initial breakup of the liquid column into droplets.
• Secondary Breakup: This is where Madabhushi is differentiated from other breakup models (incorporating Pilch and Erdman model). It considers the formation of ligaments (irregularly shaped fragments that break off from the liquid core), which is a more realistic regarding real-world scenario (See Fig. 10).

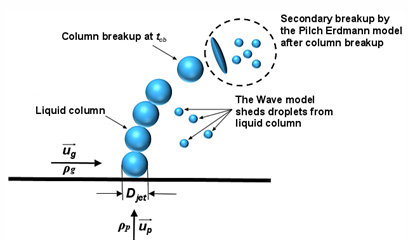
Figure 10: Madabhushi breakup model – Reference: ANSYS Help

Tip: As stated, the Madabhushi model considers the formation of ligaments. Madabhushi introduces a weighting factor for accounting the impact of ligaments on child droplet sizes.

You can read more about the governing equations in ANSYS Help. In the software, For using the Implementation of Madabhushi breakup model, we are asked to define (Fig. 11):

• B0: It is 0.61, by default. This constant affects the initial breakup behavior of the liquid column.
• B1: 1.73, by default. B1 value influences the secondary breakup process.
• C0: ANSYS considers 1.44 by default. This is the column breakup time constant. It affects the timing of the column breakup process.
• Column Drag Cd: 1.48 is the default value. Representing drag coefficient used during the column breakup phase.
• Ligament Factor: 0.4 is the default constant. It directly affects child droplet size forming in secondary breakup.
• Jet Diameter [m]: It the nozzle orifice exit diameter.
• Breakup Max Generation: It limits the number of generations of droplet breakup. It prevents excessive computational load.
• Subsequent Statistical Breakup: When enabled, this option activates a statistical breakup model after reaching the Breakup Max Generation limit. Instead of creating new child parcels, it increases the particle count within existing parcels and adjusts particle diameters, maintaining the parent parcel’s total mass throughout the breakup process.

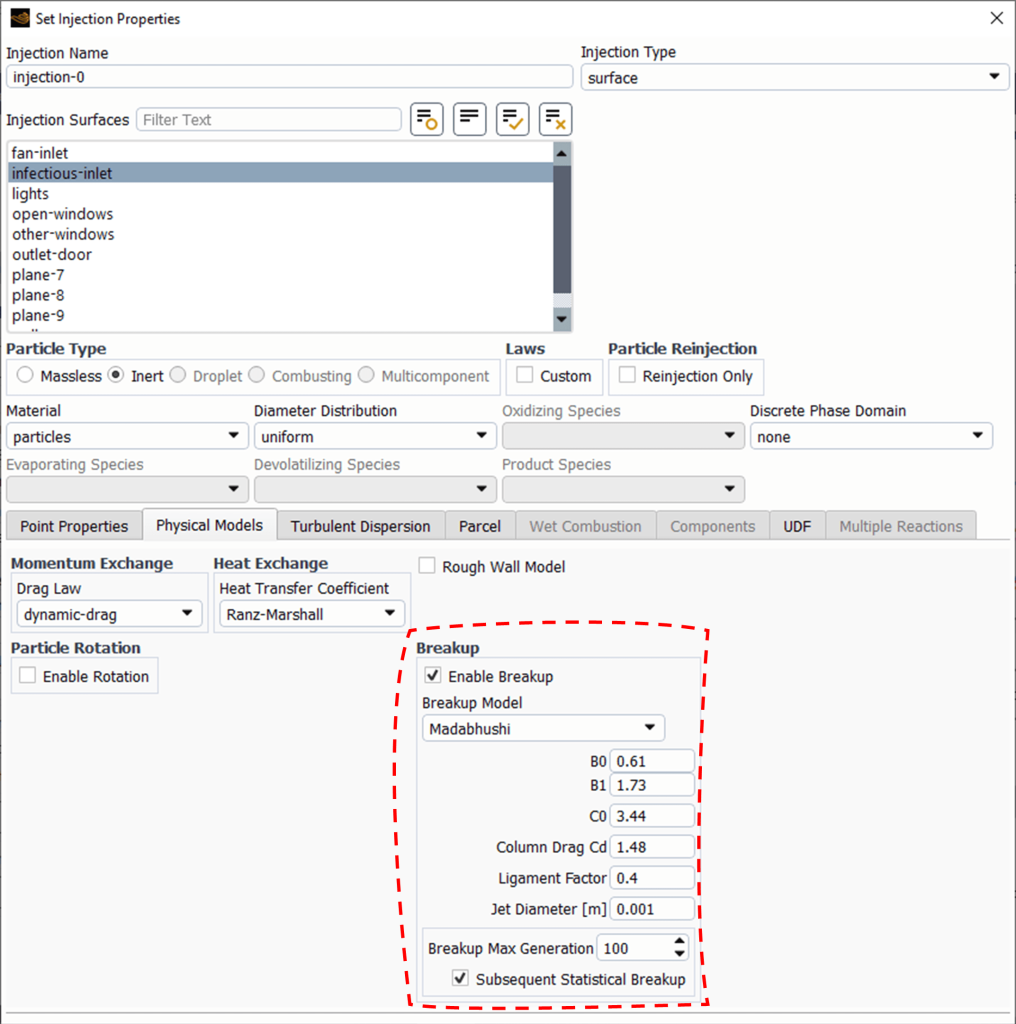
Figure 11: Madabhushi breakup model in ANSYS Fluent

 

6) Schmehl Breakup Model

Schmehl breakup model distinguishes breakup regimes into three:

• Bag Breakup
• Multimode Breakup
• Shear Breakup

These regimes are differentiated based on two dimensionless numbers:  Weber number (We) & Ohnesorge number (Oh).

Weber number is introduced in the introduction of the blog. The Ohnesorge number assesses the damping effect of viscous friction against surface tension within the droplet:

   

Where:

μ is the dynamic viscosity.

Schmehl breakup model switches between these regimes considering functions dependent on the local Weber number:

Deformation with no breakup:

Bag Breakup:

Multimode Breakup:

Shear Breakup:

Tip: Regardless of the regime, on the other hand, the Schmehl model divides the breakup process into two stages:

• Initial deformation of the droplet into a disc shape
• Further deformation with disintegration of the droplets

This two-stage approach allows for an understanding of how different forces interact to cause droplet breakup.

Tip: The behavior of child droplets formed during breakup varies across the different regimes:

In Bag Breakup and Multimode Breakup regimes, the volumetric distribution of child droplets follows a root-normal distribution, similar to the Madabhushi model:

   

Where μ is the mean and σ is the standard deviation.

But, in the Shear Breakup regime, the distribution is bimodal. Approximately 80% of the parent droplet’s mass forms small droplets due to shear forces, while the remaining 20% forms larger core droplets.

Tip: Interestingly, by setting the number of breakup parcels to 1(see Fig.1), a statistical breakup takes place without shedding child droplet parcels. Instead, the parent droplet parcel is reformed by the new diameter, flow rate, and number in the parcel. This fantastic feature provides precise control over simulation parameters.

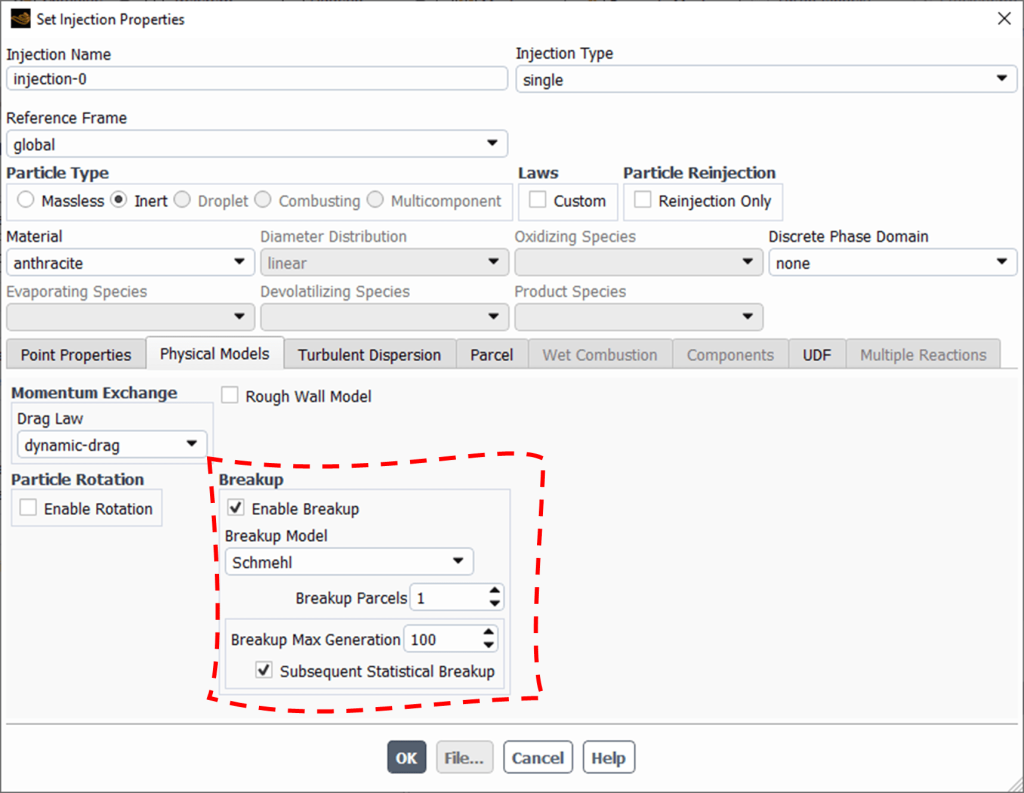
Figure 12: Schmehl breakup model in ANSYS Fluent

read more:

Grid Size Independency in Discrete Phase Model (DPM)

Discrete Phase Model Parcel Concept