Droplet evaporation is a key phenomenon in many industrial processes, including spray drying, fuel atomization, and cooling towers. Understanding the rate of evaporation and its impact on the surrounding environment is a determinant.
Contents
ToggleThis tutorial aims to guide engineers, researchers, and CFD practitioners through using DPM Droplet particle type. While DPM allows for both droplet and multi-component particle types, we will focus on the droplet type here, reserving the multi-component approach for a future discussion.
DPM Droplet Evaporation
DPM Droplet Particle Type Fundamentals
Initially, to model the evaporation of a droplet particle, the Droplet particle type must be selected in the first place, accessible from “Set Injection Properties” window (see Fig.1).
- Tip: Droplet particle usage requires definition of at least two species. One for the droplet material and the other for evaporating fraction of the droplet. Consequently, droplet particle type will be available only if Species Transport Model is primarily activated.

Figure 1: Droplet particle evaporation tutorial in ANSYS Fluent
Similar to any other particle type in ANSYS Fluent, the discrete phase particle trajectory is followed by integration of force balance on it, written in Lagrangian framework:
![]()
![]() represents the particle’s mass multiplied by its acceleration.
represents the particle’s mass multiplied by its acceleration. ![]() is the drag force, where
is the drag force, where ![]() is the fluid velocity,
is the fluid velocity, ![]() is the particle velocity, and
is the particle velocity, and ![]() is the particle relaxation time.
is the particle relaxation time. ![]() accounts for the gravitational force and buoyancy, where
accounts for the gravitational force and buoyancy, where ![]() is the gravitational acceleration,
is the gravitational acceleration, ![]() is the particle density, and
is the particle density, and ![]() is the fluid density.
is the fluid density. ![]() represents additional forces that may act on the particle, completely explained in DPM Physical Models
represents additional forces that may act on the particle, completely explained in DPM Physical Models
Now, we can swift through the basic concepts of DPM droplet evaporation process in ANSYS Fluent. The droplet evaporation must be introduced from two distinct aspects: 1) Heat Transfer 2) Mass Transfer
- Tip: In ANSYS Fluent, the condensation of droplet particles is not included unless the user utilizes a User-defined function.
Heat Transfer of DPM Droplet Evaporation
Droplet evaporation experiences several stages as it moves through the gas phase (continuous phase) regarding heat transfer. When a droplet is injected into a domain with a different temperature, heat transfer occurs due to the temperature gradient between the droplet and its surroundings. Naturally, Heat always transfers from higher to lower temperature regions. Nevertheless, in most cases, droplets are injected into a hot domain, and they experience heating, which leads to temperature increase and eventual vaporization. Fig. 2 illustrates the temperature gradient between a droplet and its ambient environment:

Figure 2: DPM Droplet evaporation due to temperature gradient
The figure shows a difference between the droplet surface (T-surface) and the ambient temperature (T-ambient). This gradient drives the heat transfer process, causing the droplet temperature to change over time.
Tip: Heat can be transferred via Convection and Radiation mechanisms.
So, how does ANSYS distinguish the governing equations in this process?
According to the ANSYS Fluent code, droplets experience 3 distinct periods after injection, each governed by specific laws and equations (see Fig. 3):
( Definition: p= droplet, vap= vaporization, bp= boiling point)

Figure 3: DPM Droplet evaporation in ANSYS Fluent
1) Inert Heating Law (Law 1):
- Condition: Tp < Tvap
Under these circumstances, the droplet temperature (Tp) increases from the injection temperature to the vaporization temperature (Tvap). (No Phase Change)
Temperature of the droplet is calculated as (regarding radiative and convective heat transfer):
![]()
2) Droplet Vaporization Law (Law 2)
- Condition: Tvap < Tp < Tbp
This stage begins when the droplet reaches the vaporization temperature and continues until it reaches the boiling point (Tbp). In this period, vaporization occurs, and the droplet’s mass decreases. Law 2 governs the process and is initiated the moment Tp=Tvap. In this region, an extra term is added due to the presence of evaporation:
![]()
Where:
 is the mass of the droplet
is the mass of the droplet is the specific heat capacity of the droplet
is the specific heat capacity of the droplet is the rate of change of temperature of the droplet
is the rate of change of temperature of the droplet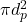 is the surface area of the droplet
is the surface area of the droplet is the heat transfer coefficient
is the heat transfer coefficient is the ambient temperature
is the ambient temperature is the temperature of the droplet
is the temperature of the droplet is the evaporation rate
is the evaporation rate is the latent heat
is the latent heat is the emissivity of the droplet
is the emissivity of the droplet is the Stefan-Boltzmann constant
is the Stefan-Boltzmann constant is the radiation temperature
is the radiation temperature
Tips: What if the droplet temperature falls below Tvap? Once law 2 is initiated, vaporization continues even if the droplet temperature falls below Tvap. It stops only if the droplet temperature falls below the dew point. In this condition, the droplet remains in law 2, but no evaporation takes place.
3) Boiling Law (Law 3)
- Condition: Tp >= Tbp
When the droplet temperature reaches the boiling point, rapid vaporization occurs. The software automatically transits Law 2 to Law 3, which predicts the boiling rate. The droplet is assumed to stay at a constant temperature while the boiling rate is applied.
Tip: Define appropriate material properties for Droplet particles, including Vaporization Temperature, Latent heat, Boiling point, and Volatile component fraction effective (Fig.4). ![]() or latent heat required for phase change from an evaporating liquid droplet. Logically, the volatile component fraction of a droplet is 100%.
or latent heat required for phase change from an evaporating liquid droplet. Logically, the volatile component fraction of a droplet is 100%.
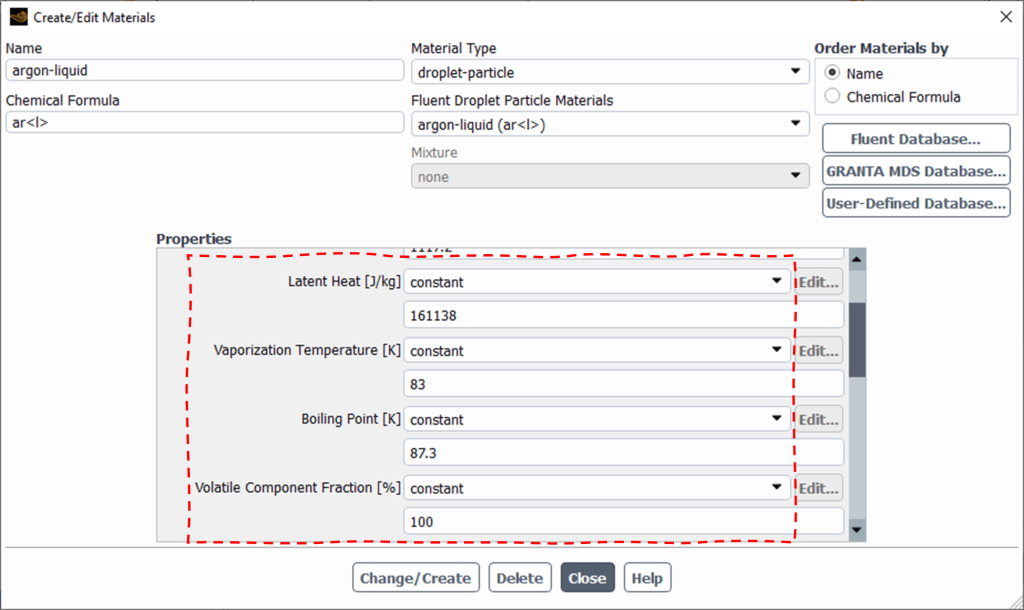
Figure 4: Material properties for DPM droplet evaporation in Fluent
In the next section, we discuss the mass transfer aspects of droplet particles, which are closely coupled with the heat transfer processes discussed here.
Mass Transfer of DPM Droplet Evaporation
The concept of concentration is the basis of mass transfer in evaporating droplets. It is the driving force for mass transfer: Difference in vapor concentration between the droplet surface and its surrounding environment.

Figure 5: Concentration gradient around an evaporating droplet
On the droplet`s surface, the vapor concentration is equal to the saturated vapor concentration. This can be expressed mathematically as:
![]()
Where:
- Ci,s is the vapor concentration at the droplet surface
- psat(Tp) is the saturation vapor pressure at the particle temperature
- R is the universal gas constant
- Tp is the particle temperature
During the vaporization process (Law 2), the vaporization rate is defined by gradient diffusion model. The fundamental equation describing this process is:
![]()
Where:
- Ni is the molar flux of vapor (kg mol/m²-s)
- kc is the mass transfer coefficient (m/s)
- Ci,s is the vapor concentration at the droplet surface (kg mol/m³)
- Ci,∞ is the vapor concentration in the bulk gas (kg mol/m³)
Finally, the mass transfer coefficient is calculated using the Sherwood number correlation:
![]()
Where:
- ShAB is the Sherwood number
- dp is the droplet diameter
- Di,m is the diffusion coefficient of vapor in the bulk
- Red is the Reynolds number based on the droplet diameter
- Sc is the Schmidt number
Tip: The fundamentals of evaporating droplets’ mass transfer have proved that it is not just about heat transfer. Actually, it is the concentration gradient that controls the evaporation process. Vaporization/Boiling Model provided in material properties for droplet particle has two predefined models: Diffusion-controlled and convection/diffusion controlled. Keep the default model for slowly evaporating droplets. The convection/diffusion-controlled model is the best choice when the evaporation rate is high. To conclude:
- Diffusion Controlled Model (Default): for low evaporation rates.
- Convection/Diffusion Controlled Model: for higher evaporation rates.
Figure 6: Vaporization/Boiling model in DPM
Tip: Additional sub-models are offered by ANSYS Fluent to enhance simulation accuracy, such as temperature-dependent latent heat, pressure-dependent boiling, and break-up models. Please visit Discrete Phase Model (DPM) Physical Models for more info.
DPM droplet evaporation Example
Here are some practical simulations related to DPM droplet evaporation. You can find more products in CFD ِDPM Projects. Drying grains for safe storage is essential in agriculture. The humid must be evaporated during the drying process, thus the droplet evaporation model is of high importance.

Figure 7: DDPM-DEM CFD Simulation of Drying of Grains, ANSYS Fluent & Matlab Coupling
The other practical application of DPM droplet evaporation is in air-cooled chillers, where water mist spray systems can be used on the condenser coils of air-cooled chillers. Notably, this simulation is conducted to validate the paper entitled “Enhancing COP of an air-cooled chiller with integrating a water mist system to its condenser: Investigating the effect of spray nozzle orientation” published in the International Journal of Thermal Sciences.

Figure 8: Water Mist Spray Nozzle Considering Evaporation Using 2 CFD-way DPM –Numerical Paper Validation
read more:

